Homework on Linear Systems of Equations Solutions
Purpose: To provide you with more practice on
reduced row-echelon form and on the parametric representations
of solutions to systems of linear equations .
1. Find an equation for the three -dimensional linear object which has three
direction vectors 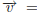
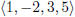 and
and 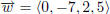 and
which passes through the point P(7, 5, 3, 1).
and
which passes through the point P(7, 5, 3, 1).
Answer: The equation is given by 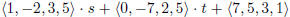 .
Thus, the
.
Thus, the
parametric form is w = s + 7, x = −2s − 7t + 5, y = 3s + 2t + 3, and z = 5s + 5t
+ 1.
2. Find the parametric form of the equation for a line in 4-D which passes
through the points P(1, 2, 3, 4)
and Q(−3, 5, 4, 1).
Answer: We can use 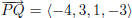 as the direction
vector and Q as the position to
as the direction
vector and Q as the position to
obtain 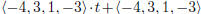 , or w = −4t−4, x = 3t+3, y = t+1, and
z = −3t−3.
, or w = −4t−4, x = 3t+3, y = t+1, and
z = −3t−3.
3. Complete the following two problems :
(a) Determine three distinct ways to balance the following chemical equation:
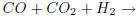 .
.
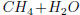 In particular, find the balanced equation in
which two (2) moles of
In particular, find the balanced equation in
which two (2) moles of 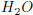 are produced
are produced
for every five (5) moles of 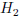 consumed.
consumed.
Answer:
Consider  . Solving the resulting system of
. Solving the resulting system of
equations results in the following matrix:
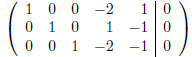
Therefore, there are two free variables , D = s and E = t,
and the rest are determined by
A = 2s−t, B = −s+t, and C = 2s+t.We can get several distinct solutions. For
example,
A = 1, B = 1, C = 7, D = 2, E = 3 and A = 2, B = 1, C = 10, D = 3, E = 4 and
A = 1, B = 2, C = 11, D = 3, E = 5 and A = 3, B = 1, C = 13, D = 4, E = 5. In
the second, the ratio between water produced and hydrogen consumed is 2 to 5.
(b) Using systems of equations , balance the following chemical equation:
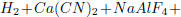
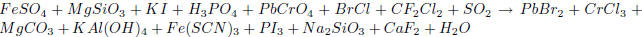
Answer: 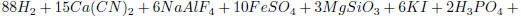
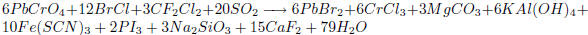
4. For each of the following augmented matrices:
(a) Tell whether it is in row- reduced form .
(b) If not, state which part of the definition it violates and put it in
row- reduced form .
(c) Identify the dimension of the solution space from the reduced matrix.
(d) Write the parametric form and the vector parametric form of the solution to
the system of equations .

Answer:
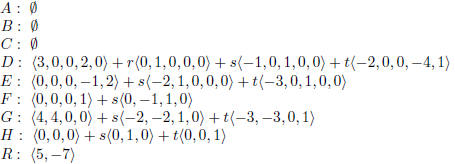
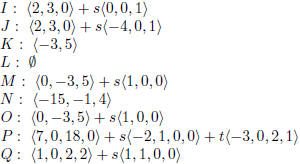
| Prev | Next |