Rational Numbers & Periodic Decimal Expansions
A rational number is one that can be expressed as the ratio of two
integers (i.e., whole
numbers), for example, 1/2 or 2/3. A real number that is not a rational number
is referred to
as an irrational number.
Not all real numbers are rational — in fact, most are not. This is not
immediately obvious
since the rational numbers can easily serve many practical purposes. We
formalize this
claim as an assertion to be proven.
Assertion: The
 is not a rational number.
is not a rational number.
Proof:
This is a proof by contradiction. That is, we assume that
 is rational, and see that this
is rational, and see that this
inescapably leads us to a conclusion that is impossible, and that forces this
assumption
to be false. So we suppose that
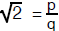 for some integers p and q. Without loss of
for some integers p and q. Without loss of
generality, we can also assume that p and q have no factors in common (since any
common factors could be cancelled without changing the ratio). Now we do a
little algebra,
first squaring both sides of the equation to conclude that
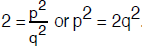 But then
But then
since p2 is even, it must be that p is also even (if p were odd, then p2 is the
product of
two odds and must also be odd), say p = 2r. Now one more algebraic step, namely
p2 =
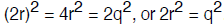 Now we can again claim that since q2 is even, it must be
Now we can again claim that since q2 is even, it must be
that q is even. But this means that p and q have the factor 2 in common
contradicting our
initial assumption. Hence no such integers p and q can exist to express
 as a ratio,
as a ratio,
and so
 is irrational.
is irrational.
Of course, this only establishes the existence of a single irrational number.
But it is not
difficult to repeat this argument to show many numbers are irrational. This can
be done for
other “ roots ”, the mathematical constants p and e (base of natural logarithms),
etc.
The main point in this note is to show there is a perfect correspondence
between the
rational numbers and the numbers with periodic or finite decimal expansions .
That is,
numbers such as 1/3 have the unending, but repeating, decimal expansion .333 … .
Often
to provide a precise but succinct way to write such decimal expansions, the
repeating
part is written only once and marked with an overbar. For instance,
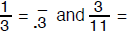
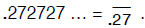 Finite decimal expansions such as
Finite decimal expansions such as
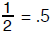 could be regarded as
could be regarded as
repeating, where the repeating part is 0. Therefore they need no special
attention.
Assertion: Each rational number has a periodic decimal expansion, and every
number with
a periodic decimal expansion is a rational number.
Proof:
This proof comes in two parts. First we see that each rational has a periodic
decimal
expansion. Then we show that every periodic decimal expansion can be expressed
as
the ratio of two integers.
Part I: each rational p/q has either a finite or a periodic infinite
decimal expansion.
This is evident if we visualize carrying out the familiar division algorithm . We
illustrate this
on one specific example here, but the analysis is fully general. Consider
carrying out the
division 5/12. This can be presented in the customary format as
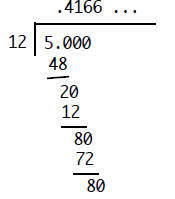
Notice that at this point the remainder of 8 has repeated. From this point
on, this repetition
will continue without end. Hence we have the repeating decimal expansion
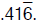
In general for a rational p/q the remainder must be less than q. If a
remainder of zero occurs ,
the process terminates with a finite expansion. Otherwise, after at most q steps
a
repetition of a non-zero remainder must occur. Once this happens we have an
unending
series of these repetitions giving an infinite repeating decimal expansion.
Part II: each number with a finite or periodic infinite decimal
expansion is a rational number.
For finite expansions, the result is immediate so we focus on infinite periodic
expansions.
To prove this case we need a couple of helping results. The first is about
geometric sums.
Lemma 1: for any number x≠1 and any integer
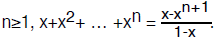
You are probably familiar with this result, and if not we will present its
proof a little later in
this course. The second result uses the first and concerns infinite geometric
sums.
Lemma 2: for any number x whose absolute value is less than 1,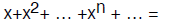
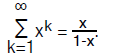
This result follows from Lemma 1 since the limit of xk is 0 as k tends to
infinity when |x|<1.
This allows us to convert any periodic infinite decimal expansion into its
rational number
equivalent . For instance,
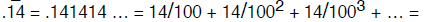
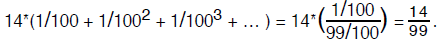 If you’re not convinced
by this,
If you’re not convinced
by this,
try computing the decimal expansion of 14/99.
We can conclude that irrational numbers have no natural
finite representation — they have
infinite non-repeating decimal expansions. The computing implications of this
conclusion are
that common calculations , even those starting with rational numbers, may easily
lead to
numeric results that have no representation that can be readily stored in a
computer and
are impossible to compute precisely!
Since many numbers (e.g.,
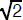 ) cannot be computed exactly, we must often
settle for
) cannot be computed exactly, we must often
settle for
approximations. For example, to compute the 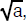 ,
we begin with an initial approximation
,
we begin with an initial approximation
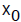 , and then continue to
obtain better approximations using the formula
, and then continue to
obtain better approximations using the formula
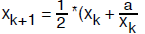 ,
,
for k = 0, 1, 2, …, until 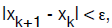 where e is the
desired degree of accuracy. For
where e is the
desired degree of accuracy. For
instance, to obtain 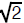 , take x0 = 1, and then
, take x0 = 1, and then
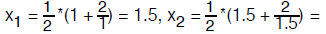
 , etc. The development of such
, etc. The development of such
approximation techniques and the study of how rapidly they converge constitutes
the field
of numerical analysis. This area is concerned with the real (i.e., rational plus
irrational)
numbers, a set which is not discrete. Real numbers must be described by limiting
techniques such as
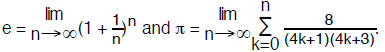
| Prev | Next |