Mathematics Practices
Exploration 15-6a: Rehearsal #1 for Test
Objective: Analyze polynomial functions and their rates of change.
|
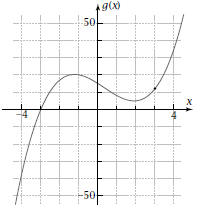
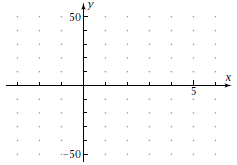
Answer all of these questions on separate paper. You may draw graphs on this sheet where specified. 1. Let 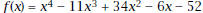 Plot the graph Plot the graphof f. Sketch the result here.
2. By synthetic substitution , show that 2 is a
zero of
|
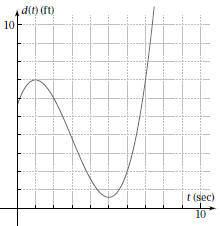
For Problems 9–14, a freight train backs up, stops, and then goes forward. The displacement, 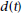 kilometers, of
kilometers, ofits engine from a railroad crossing is given by
9. What is the average velocity of the train from |
Exploration 15-6b: Rehearsal #2 for Test
Objective: Analyze polynomial functions and their rates of change
|
1. Mr. X, the math teacher, is making up a test for his students. He wants them to find the particular equation of a cubic function, but all he will reveal about it is that for its three zeros, is true:
Find the particular equation for
2. One of the zeros of
6. Let |
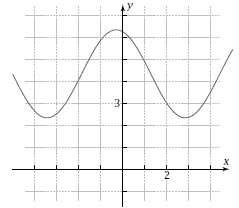
8. On this set of axes, sketch the graph of h.
9. At a double zero, the graph of a polynomial
function
10. What is its average velocity from
|
Exploration 15-6c: Rehearsal #3 for Test, Date:
Annotated List
Objective: Analyze polynomial functions and their rates of change.
|
1. Find the particular equation of a polynomial function. a. From points, e.g., a cubic function containing the points (2, 7), (3, 34), (4, 91), and (5, 190). b. From zeros, e.g., a cubic function with leading coefficient 1 and zeros -5, 3, and 6. Write in factored form and then multiply and simplify . Confirm by graphing. c. From sums and products of zeros, e.g., sum= 1, product = -15, sum of pairwise products = -7. 2. Find zeros of a polynomial function. a. By graphing, e.g., 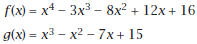 Explain how you know that two of the zeros of b. By synthetic substitution, e.g., 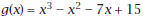 Find the complex zeros using the quadratic formula. 3. Find discontinuities in a rational function . a. Vertical asymptotes, e.g.,
|
remove the removable discontinuity. Use the simplified equation to calculate the instantaneous velocity at 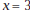 exactly. exactly.d. Instantaneous rate by shortcut, e.g., let 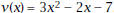 . Show that . Show that
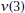 equals the equals theinstantaneous rate of change of 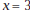 Explain how you can find the equation for 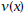 from the equation for e. Instantaneous rate graphically, e.g., the figure here shows the graph of the graph at the point 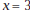 with slope
equal to the with slope
equal to theinstantaneous rate of change of How is the line related to the graph?
|
| Prev | Next |
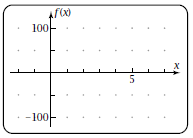
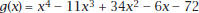 Plot the graph
Plot the graph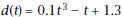
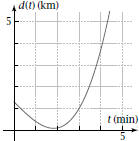
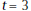 to
to
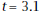 minutes? What is the average
velocity
minutes? What is the average
velocity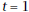 minute, is the train
approaching the
minute, is the train
approaching the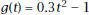 Find
Find
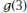 and
and
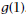 .Show that
.Show that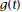 in Problem 13 is the velocity
function. At what
in Problem 13 is the velocity
function. At what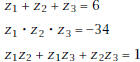
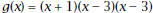 has a double zero
has a double zero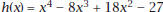 . By
synthetic
. By
synthetic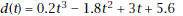
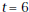 to
to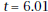 seconds?
seconds?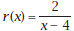
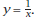
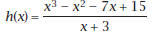
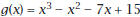 where x is in seconds. Find
where x is in seconds. Find