EXISTENCE AND UNIQUENESS OF A COMPLETE ORDERED FIELD

This appendix is devoted to the proofs of Theorems 1.1 and 1.2, which together
assert that there exists a unique complete ordered field . Our construction of this
field will follow the ideas of Dedekind, which he presented in the late 1800's.

DEFINITION. By a Dedekind cut, or simply a cut, we will mean a pair (A, B)
of nonempty (not necessarily disjoint) subsets of the set Q of rational numbers for
which the following two conditions hold.

(1) A ∪ B = Q. That is, every rational number is in one or the other of these
two sets.
(2) For every element a ∈A and every element b ∈ B, A ≤ b. That is, every
element of A is less than or equal to every element of B.
Recall that when we define the rational numbers as quotients (ordered pairs)
of integers, we faced the problem that two different quotients determine the same
rational number, e.g., 2/3 ≡ 6/9. There is a similar equivalence among Dedekind
cuts.

DEFINITION. Two Dedekind cuts (A₁, b₁) and (A₂,B₂) are called equivalent if
a₁ ≤ b₂ for all a₁ ∈ A₁ and all b₂ ∈B₂, and a₂ ≤b₁ for all a₂ ∈ A₂ and all b₁ ∈ B₁.
In such a case, we write (A₁,B₁) ≡ (A₂,B₂).

bf Exercise A.1. (a) Show that every rational number r determines three distinct
Dedekind cuts that are mutually equivalent.

(b) Let B be the set of all positive rational numbers r whose square is greater
than 2, and let A comprise all the rationals not in B. Prove that the pair (A, B) is
a Dedekind cut. Do you think this cut is not equivalent to any cut determined by
a rational number r as in part (a)? Can you prove this?

(c) Prove that the definition of equivalence given above satisfies the three conditions
of an equivalence relation. Namely, show that
(i) (Re exivity) (A,B) is equivalent to itself .
(ii) (Symmetry) If (A₁,B₁) ≡ (A₂,B₂), then (A₂,B₂) ≡ (A₁,B₁).
(iii) (Transitivity) If (A₁,B₁) ≡ (A₂,B₂) and (A₂,B₂) ≡ (A₃,B₃), then (A₁,B₁)
≡ (A₃,B₃).

There are three relatively simple -sounding and believable properties of cuts , and
we present them in the next theorem. It may be surprising that the proof seems to
be more difficult than might have been expected.

THEOREM A.1. Let (A, B) be a Dedekind cut. Then
(1) If a ∈ A and a' < a, then a' ∈ A.
(2) If b ∈ B and b' > b, then b' ∈ B.
(3) Let be a positive rational number. Then there exists an a ∈ A and a b ∈ B
such that b - a < ε.

PROOF. Suppose a is an element of A, and let a' < a be given. By way of
contradiction suppose that a' does not belong to A. Then, by Condition (1) of
the definition of a cut, it must be that a' ∈B. But then, by Condition (2) of the
definition of a cut, we must have that a ≤ a', and this is a contradiction, because
a' < a. This proves part (1). Part (2) is proved in a similar manner.

APPENDIX

To prove part (3), let the rational number ε > 0 be given, and set r = ε/2.
Choose an element a₀ ∈ A and an element b₀ ∈ B. Such elements exist, because A
and B are nonempty sets. Choose a natural number N such that a₀ + Nr > b₀.
Such a natural number N must exist. For instance, just choose N to be larger than
the rational number (b₀-a₀)/r. Now define a sequence {a_k} of rational numbers by
a*k = a₀ + kr, and let K be the first natural number for which a_k ∈ B. Obviously,
such a number exists, and in fact K must be less than or equal to N. Now,
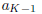
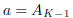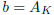is not in B, so it must be in A. Set and . Clearly, a ∈ A, b ∈ B,
and

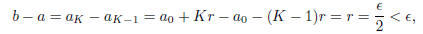
and this proves part (3).

We will make a complete ordered field F whose elements are the set of equivalence
classes of Dedekind cuts. We will call this field the Dedekind eld. To make this
construction, we must define addition and multiplication of equivalence classes of
cuts, and verify the six required field axioms. Then, we must define the set P that
is to be the positive elements of the Dedekind field F, and then verify the required
properties of an ordered field. Finally, we must prove that this field is a complete
ordered field, i.e., that every nonempty set that is bounded above has a least upper
bound. First things first.

DEFINITION. If (A₁,B₁) and (A₂,B₂) are Dedekind cuts, define the sum of
(A₁,B₁) and (A₂,B₂) to be the cut (A₃,B₃) described as follows. B₃ is the set of
all rational numbers b₃ that can be written as b₁+b₂ for some b₁ ∈ B₁ and b₂ ∈ B₂,
and A₃ is the set of all rational numbers r such that r < b₃ for all b₃ ∈ B₃.

Several things need to be checked. First of all, the pair (A₃,B₃) is again a
Dedekind cut. Indeed, it is clear from the definition that every element of A₃ is
less than or equal to every element of B₃, so that Condition (2) is satisfied. To see
that Condition (1) holds, let r be a rational number, and suppose that it is not in
A₃. We must show that r belongs to B₃. Now, since r 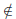A₃, there must exist an
element b₃ = b₁ + b₂ ∈B₃ for which r > b₃. Otherwise, r would be in A₃. But this
means that r - b₂ > b₁, and so by part (2) of Theorem A.1, we have that r - b₂ is
an element b'₁ of B₁. Therefore, r = b'₁ + b₂, implying that r ∈ B₃, as desired.

We define the 0 cut to be the pair A₀ = {r : r ≤ 0} and B₀ = {r : r > 0}. This
cut is one of the three determined by the rational number 0.
bf Exercise A.2. (a) Prove that addition of Dedekind cuts is commutative and
associative.
(b) Prove that if (A₁,B₁) ≡ (C₁,D₁) and (A₂,B₂)  ≡ (C₂,D₂), then (A₁,B₁) +
(A₂,B₂)  ≡ (C₁,D₁) + (C₂,D₂).
(c) Find an example of a cut (A, B) such that (A, B) + 0 ≠ (A, B).
(d) Prove that (A, B) + 0 ≡ (A, B) for every cut (A, B).

We define addition in the set F of all equivalence classes of Dedekind cuts as
follows.

DEFINITION. If x is the equivalence class of a cut (A, b) and y is the equivalence
class of a cut (C, D), then x+y is the equivalence class of the cut (A, B)+(C, D).

It follows from the previous exercise, that addition in F is well-defined, commutative,
and associative. We are on our way.

We define the element 0 of F to be the equivalence class of the 0 cut. The next
theorem establishes one of the important field axioms for F, namely, the existence
of an additive inverse for each element of F.

THEOREM A.2. If (A, B) is a Dedekind cut, then there exists a cut (A', B')
such that (A, B) + (A', B') is equivalent to the 0 cut. Therefore, if x is an element
of F, then there exists an element y of F such that x + y = 0.

PROOF. Let A' = -B, i.e., the set of all the negatives of the elements of B, and
let B' = -A, i.e., the set of all the negatives of the elements of A. It is immediate
that the pair (A', B') is a Dedekind cut. Let us show that (A, B) + (A', B') is
equivalent to the zero cut . Let (C, D) = (A, B) + (A', B'). Then, by the definition
of the sum of two cuts , we know that D consists of all the elements of the form
d = b + b' = b - a, where b ∈ B and a ∈ A. Since a ≤ b for all a ∈ A and b ∈ B,
we see then that the elements of D are all greater than or equal to 0. To see that
(C, D) is equivalent to the 0 cut, it will suffice to show that D contains all the
positive rational numbers. (Why?) Hence, let ε > 0 be given, and choose an a ∈ A
and a b ∈ B such that b - a < ε. This can be done by Condition (3) of Theorem
A.1. Then, the number b - a ∈ D, and hence, by part (2) of Theorem A.1, ε ∈ D.
It follows then that the cut (C, D) is equivalent to the zero cut (A₀, B₀), as desired.

We will write -(A, B) for the cut (A',B') of the preceding proof.

bf Exercise A.3. (a) Suppose (A, B) is a cut, and let (C, D) be a cut for which
(A, B) + (C, D) is equivalent to the 0 cut. Show that (C, D) (A', B') = -(A, B).

(b) Prove that the additive inverse of an element x of the Dedekind field F is
unique.

The definition of multiplication of cuts, as well as multiplication in F, is a bit
more tricky. In fact, we will first introduce the notion of positivity among Dedekind
cuts.

DEFINITION. A Dedekind cut x = (A, B) is called positive if A contains at
least one positive rational number.

bf Exercise A.4. (a) Suppose (A, B) and (C, D) are equivalent cuts, and assume that
(A, B) is positive. Prove that (C, D) also is positive. Make the obvious definition
of positivity in the set F.

(b) Show that the sum of two positive cuts is positive. Conclude that the sum of
two positive elements of F, i.e., the sum of two equivalence classes of positive cuts,
is positive.

(c) Let (A, B) be a Dedekind cut. Show that one and only one of the following
three properties holds for (A, B). (i) (A, B) is a positive cut, (ii) -(A, B) is a
positive cut, or (iii) (A, B) is equivalent to the 0 cut.

(d) Establish the law of tricotomy for F . That is, show that one and only one
of the following three properties holds for an element x ∈ F. (i) x is positive, (ii)
-x is positive, or (iii) x = 0.

We first define multiplication of cuts when one of them is positive.

DEFINITION. Let (A₁,B₁) and (A₂,B₂) be two Dedekind cuts, and suppose
that one of these cuts is a positive cut. We define the product (A₃,B₃) of (A₁,B₁)
and (A₂,B₂) as follows. Set B₃ equal to the set of all b₃ that can be written as
b₁b₂ for some b₁ ∈ B₁ and b₂ ∈ B₂. Then set A₃ to be all the rational numbers r
for which r < b₃ for all b₃ ∈ B₃.

Again, things need to be checked.

bf Exercise A.5. (a) Show that the pair (A₃,B₃) of the preceding definition for the
product of positive cuts is in fact a Dedekind cut.

(b) Prove that multiplication of Dedekind cuts, when one of them is positive, is
commutative.

(c) Suppose (A₁,B₁) is a positive cut. Prove that

(A₁,B₁)((A₂,B₂) + (A₃,B₃)) = (A₁,B₁)(A₂,B₂) + (A₁,B₁)(A₃,B₃)

for any cuts (A₂,B₂) and (A₃,B₃).

(d) Show that, if (A₁,B₁) ≡ (A₂,B₂) and (C₁,D₁) ≡ (C₂,D₂) and (a₁,B₁) and
(A₂,B₂) are positive cuts, then (A₁,B₁)(C₁,D₁) ≡ (A₂,B₂)(C₂,D₂).

(e) Show that the product of two positive cuts is again a positive cut.

We are ready to define multiplication in F.