Rational Functions
I got the following question by email today. I think a lot
of you may have a similar question, so
I'm answering it here.
Brad- I didn't get the chance to ask you in class the other day, but could you
please
explain to me again how you find the limit of a complex rational ? And also how
one
can graph this limit. Thank you.
I'll answer the two questions I think you might be asking.
1. How do you find the limit, as x approaches c, of a rational function?
Say the rational function is p(x)/q(x), where p and q are polynomials.
Solution : Try substituting c for x .
•
If q(c) ≠ 0, you have your limit: p(c)/q(c). Problem solved .
•
On the other hand, if the denominator is zero , it gets a little more
interesting. The
rational function is not defined at x = c (because dividing by zero is never
stylish), but
the limit may or may not exist. This breaks down into two cases:
(a) The numerator, p(c), is also zero. This means we're looking at the
"indeterminate"
0/0 case. It's an algebraic fact (called the Fundamental Theorem of Algebra)
that
whenever c is a root of a polynomial (such as p or q), the quantity (x-c) is a
factor
of that polynomial. So, if q(c) = 0, you can rewrite q(x) as
q(x) = (x - c)(some other polynomial):
Using this idea: if plugging in c for x gives us 0/0, then c is a root of both
polynomials.
Therefore (x - c) is a factor of both polynomials. Factor it out on top and
bottom,
cancel, and start over. (There is a chance that by cancelling this factor, you
have
changed the behavior of the function at x = c-but changing the behavior at a
single point has absolutely no effect on the limit, as described at the top of
p.53.)
See example 5 on p.54, or 1.5 #37-44.
(b) p(c) ≠ 0. In this case, the limit doesn't exist. We want to be more specific
than
this, if at all possible. The limit could be: ∞, -∞, or neither. The examples in
the
book don't fully explore this, but Example 10 on p.57 is a start. Let me give
you
another example:
Find 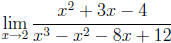 .
.
To find the limit, we start by trying the substitution x = 2. Our rational
function
becomes
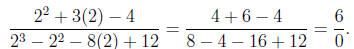
At this point we know the limit doesn't exist, because 6/0 is not a real number .
Nevertheless, we should see if we can learn anything more precise. One of the
best
ways to get information about a rational function is to factor it. Now, the
numerator
is a quadratic . We can factor that without too much trouble. The hard part is
the
denominator, a cubic. However, we know that 2 is a root of it, since setting x =
2
makes it zero. Thus, x-2 is a factor. You may use long division, synthetic
division,
or something else to factor it: x3 -x2 -8x+12 = (x-2)(x2 +x-6). (Personally, I
use "something else"...but that's another blog.) It's not too hard to finish
factoring
the denominator: (x-2)(x2 +x-6) = (x-2)(x-2)(x+3) = (x-2)2(x+3). Our
whole rational function is now
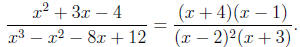
Let's recall the big picture: we know that x = 2 is a
vertical asymptote for this
graph, because when we set x = 2, the function took the form (nonzero number
over
zero). Now we want to determine how the graph behaves near the asymptote, on
each side of it. The options for each side are to dive to -∞ or to skyrocket to
∞.
If both sides go up, the limit is ∞, if both sides go down, the limit is -∞, if
one
goes up and the other down, then we simply say the limit does not exist. (Read
the
Study Tip on p.57.)
So how do we determine which infinity the function approaches? It's all a
question
of sign. As the function gets close to the vertical asymptote x = 2, is the
curve
above the x-axis, or below it? The only ways for a function to get across the
x-axis
are (1) to actually cross it (creating an x-intercept in the process), or (2) to
jump
over it (at a discontinuity). The "actual crossings" happen when y = 0, and this
happens only when the numerator is zero. A discontinuity happens only when the
denominator is zero. Thus, if we find the roots of the numerator and denominator,
then we have found the only values of x at which the sign of y could change. In
the
current example, those roots are -4, 1, 2, and -3.
These four numbers break the real line into five pieces: (-∞,-4), (-4,-3), (-3,
1),
(1, 2), and (2,∞). The only intervals here that interest me are the ones very
close to
the x = 2 asymptote, that is, (1, 2) and (2,∞). We know that the function cannot
change sign inside either of these intervals (because we've identified the only
four
points where a sign change could happen, and they aren't inside those
intervals).
Now we imagine that x is somewhere inside the interval (1, 2), and look back at
our
factored rational function. Sign is the only thing I care about now, so while I
could
pick a specific number for x (say 1.5) and get the value
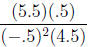
for our function, that's way too much number crunching for me. All I care about
is
whether each quantity is positive or negative for x values in the chosen
interval:
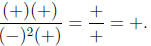
That is, as x approaches 2 from the left, our rational function remains
positive|
which means it approaches positive ∞.
For x approaching 2 from the right, I think of x as belonging to the interval
(2,∞),
which lies on the right side of 2, and check the sign of the result:
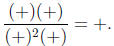
As x approaches 2 from the right, we again have a limit of positive ∞. Since the
two one-sided limits agree, we say that
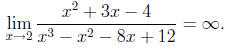
2. How do you find the limit, as x approaches ± ∞, of a
rational function?
In my opinion, this is an easier question to answer than the previous one .
Solution:
First - when I am considering a limit as x→ ± ∞, this is one of the few times when
I do not
try factor polynomials in the usual sense. The "factoring" we do is much easier,
once you get
the hang of it, you never need to think about FOIL or diamond problems or
divisibility or
any of the stuff that makes factoring hard.
We would like to find the limit as x approaches ∞ of some rational function. One
method
(with many variations) is to factor, out of top and bottom, the highest power of
x that appears
in each. Consider the problem:
Find 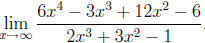
In this case, we identify 6x4 as the dominant term upstairs and 2x3 as the
dominant term
downstairs. That is, the highest power of x appearing is x4 on top and x3 on the
bottom
(at this point I don't worry too much about their coefficients, because I'm trying
to keep life
simple). Now I factor x4 out of the numerator and x3 out of the denominator, and
simplify. (If
you have trouble going left to right in the first line below, try multiplying out
the numerator
on the right side to confirm that it matches the numerator on the left, and same
for the
denominators.)
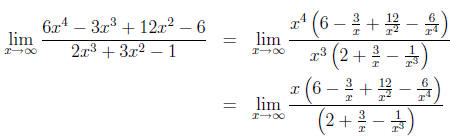
Now, as x grows, all of the little fractions shrink ( fixed numerator, big
denominator). That
is:
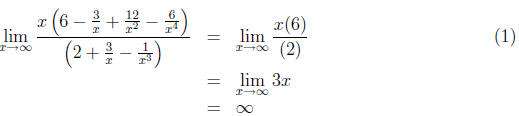
...and we are done. One shortcut, based on this method, says that if the degree
upstairs (in
this case 4) is greater than the degree downstairs (in this case 3), then the
limit will always
be either ∞ or -∞, and that you can decide which it is by comparing the leading coefficients
(in this case 6 and 2). If they have the same sign, as in this case, the limit
in ∞, if they
have different signs, the limit is -∞. I don't personally rely on this shortcut,
because the
kind of factoring we did is extremely fast when you get used to it-and because,
for limits as
x → -∞, the shortcut needs some careful buttressing. It gets a little too
confusing for my
poor brain. The method I use works to the right and the left, with no exceptions
or special
cases to worry about.
But I should give you a disclaimer about something I did during that method. Did
you notice
how I disposed of the little fractions in (1) above while keeping the front x in
the formula?
This amounts to sending some x's to infinity before I send
others. That is not always a safe
thing to do. For example, the same reasoning would show that:
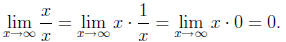
The correct value of that limit is one, not zero!
Nevertheless, the simplifications in the method
are valid as demonstrated. I'm happy to talk about the theory with anyone who
wants to
know.
Let's see another example:
Find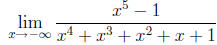 .
.
According to the method, we factor x5 from the top and x4 from the bottom,
simplify, discard
negligible fractions, and evaluate:
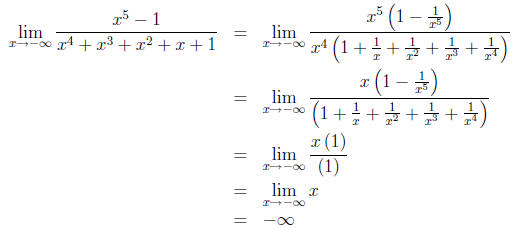
I have one more disclaimer, aimed at people who suffer from the same confusion I
had during
calculus (and for some time afterward). By reading the above sequence of
equations, you
could rightly conclude that
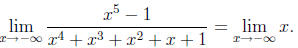
But it would not be correct to say that the functions y =
(x5 -1)/(x4 +x3 +x2 +x+1) and
y = x get arbitrarily close together as x heads for -∞. You may confirm (by long
division,
synthetic division, multiplication, extreme cleverness, or something else) that,
in actual fact,
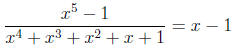
for all x. So the two functions remain exactly one unit apart. If this kind of
thing interests
you, then by all means: find the paradox in what just happened, and then explain
why there's
no paradox at all.
| Prev | Next |