Synthetic Substitution Examples and Polynomial Theorems
Consider :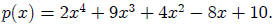
What is 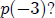
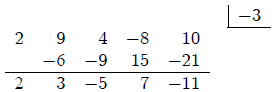
What is 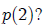
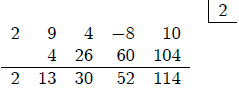
Note that 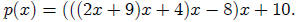
If we substitute either x=-3 or x=2 into the parenthesized
expression we can see that the numbers
that appear in the 2nd and 3rd rows of the Synthetic Substitution process really
come out of these direct
substitutions and calculations. It is for this reason that we prefer to use the
term Synthetic Substitution
as opposed to Synthetic Division whenever we calculate and fill in a table like
those above. In fact, it is
most instructive to directly substitute B instead of a number to fill in a
Synthetic Substitution table like
the one shown below. Counting the number of B's that follow each coefficient in
parentheses in the last
entry shows that the final polynomial is the same as
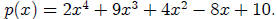
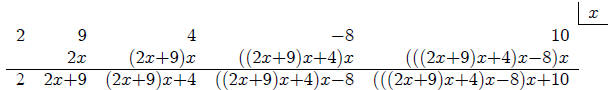
Now consider the long division of p(x) by x + 3.
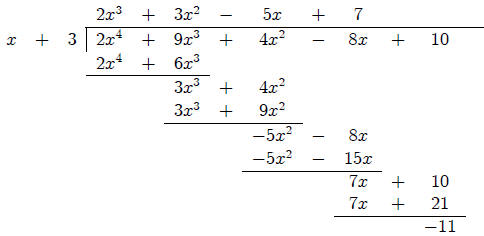
Note the coefficients in the quotient polynomial are the
same as the first numbers in the last row of the
first table above. Also note that the remainder is -11 and this is the last
number in the third row of the
first table above. These are reasons why some people use the term Synthetic
Division
Next consider the polynomial that is the product of the following 4 linear factors:
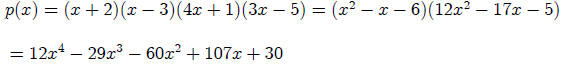
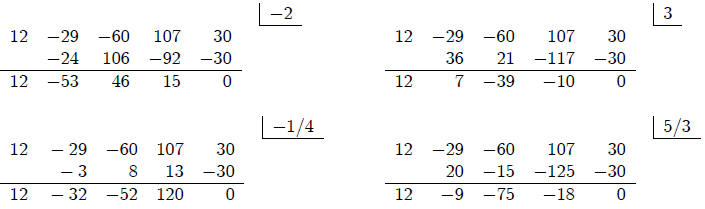
Note that the product of the four roots is: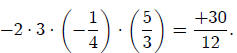
The sum of the four roots is: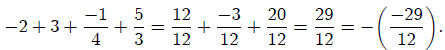
The next computations illustrate the analysis of Upper and Lower bounds.
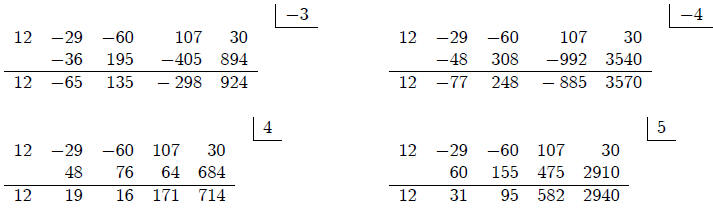
Next, consider the polynomial
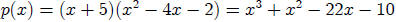
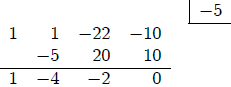
We can also substitute with irrational numbers.
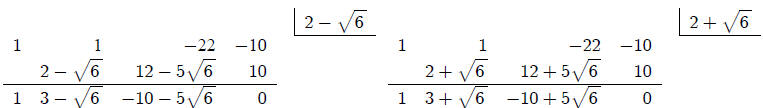
Note that the product of the three roots is:
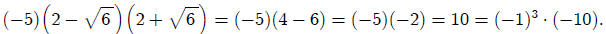
The sum of the roots is 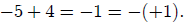
Next, consider the polynomial
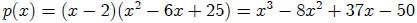
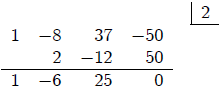
We can also substitute with complex numbers.
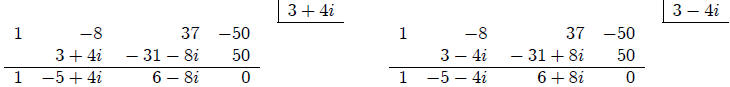
Note that the product of the three roots is:
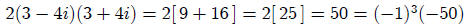
The sum of the three roots is: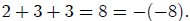
The following 31 items summarize some of the most
important theorems about polynomials. See the
note at the end of this list if you are interested in reading any of the
detailed proofs of these theorems.
1. The Division Algorithm
If 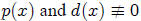 are any two polynomials then there
exist unique polynomials q(x) and r(x)
are any two polynomials then there
exist unique polynomials q(x) and r(x)
such that 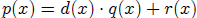 where the degree of
r(x) is stricly less than the degree of d(x)
where the degree of
r(x) is stricly less than the degree of d(x)
when the degree of 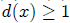 or else
or else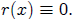
2. The Division Check for a Linear Divisor
Consider dividing the polynomial p(x) by the
linear term (x-a) Then, the Division Check
states
that: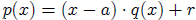
3. Remainder Theorem
When any polynomial p(x) is divided by (x-a) the remainder is
p(a)
4. Factor Theorem
(x-a) is a factor of the polynomial
p(x) if and only if p(a) = 0
5. Maximum Number of Zeros Theorem
A polynomial cannot have more real zeros than its degree.
6. Fundamental Theorem of Algebra
a) Every polynomial of degree 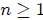 has at
least one zero among the complex numbers.
has at
least one zero among the complex numbers.
b) If p(x) denotes a polynomial of degree 8ß then
p(x) has exactly 8 roots, some of
which may be either irrational numbers or complex numbers.
7. Product and Sum of the Roots Theorem
Let 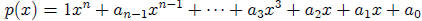 be any polynomial with real
be any polynomial with real
coefficients with a leading coefficient of 1 where
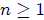 . Then
. Then 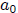 is
is
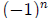 times the product of all
times the product of all
the roots of p(x) = 0 and
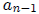 is the opposite of the sum of all the roots
of p(x) = 0
is the opposite of the sum of all the roots
of p(x) = 0
8. Rational Roots Theorem
Let 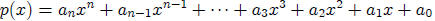 be any polynomial
be any polynomial
with integer coefficients. If the reduced rational number
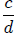 is a root of
p(x) = 0 then must be a -
is a root of
p(x) = 0 then must be a -
factor of a0 and d must be a factor of an
9. Integer Roots Theorem
Let :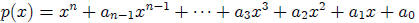 be any polynomial
be any polynomial
with integer coefficients and with a leading coefficient of 1. If
p(x) has any rational zeros,
then those zeros must all be integers.
10. Upper and Lower Bounds Theorem
Let p(x) be any polynomial with real
coefficients and a positive leading coefficient.
(Upper Bound) If 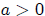 and
and
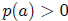 and if in applying synthetic substitution to
computep(a) all
and if in applying synthetic substitution to
computep(a) all
numbers in the 3rd row are positive, then + is an upper bound for all the roots
of p(x) = 0
(Lower Bound) If 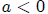 and
and
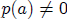 and if in applying synthetic substitution to
compute p(a) all
and if in applying synthetic substitution to
compute p(a) all
the numbers in the 3rd row alternate in sign then + is a lower bound for all the
roots of p(x) = 0
[ In either bound case, we can allow any number of zeros in any positions in the
third row except in
the first and last positions. The first number is assumed to be positive and the
last number is
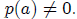 For upper bounds, we can state alternatively
and more precisely that no negatives are
For upper bounds, we can state alternatively
and more precisely that no negatives are
allowed in the 3rd row. In the lower bound case the alternating sign requirement
is not strict either,
as any 0 value can assume either sign as required. In practice you may rarely
see any zeros in the
3rd row. However, a slightly stronger and more precise statement is that the
bounds still hold even
when zeros are present anywhere as interior entries in the 3rd row.]
11. Intermediate Value Theorem
If p(x) is any polynomial with real
coefficients, and if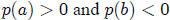 then
then
there is at least one real number - between + and , such that
p(c) = 0
12. Single Bound Theorem
Let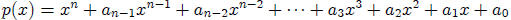 be any polynomial with
be any polynomial with
real coefficients and a leading coefficient of 1. Let
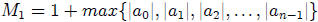 and
and
let 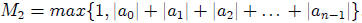 . Finally let
. Finally let
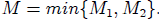 Then every
Then every
zero of p(x) lies between
-M and M.
13. Odd Degree Real Root Theorem
If p(x) has real coefficients and has a
degree that is odd then it has at least one real root.
14. Complex Conjugate Roots Theorem
If p(x) is any polynomial with real
coefficients, and if 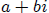 , is a complex
root of
, is a complex
root of
the equationp(x) = 0 then another complex root is its
conjugate 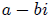
(Complex number roots appear in conjugate pairs)
15. Linear and Irreducible Quadratic Factors Theorem
Let p(x) be any polynomial with real
coefficients. Then p(x) may be written as a
product of linear
factors and irreducible quadratic factors. The sum of all the degrees of these
component factors is
the degree of p(x)
16. Irrational Conjugate Roots Theorem
Let p(x) be any polynomial with
rational real coefficients. If 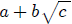 is a root of
the
is a root of
the
equation p(x) = 0 where
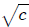 is irrational and + and , are rational, then
another root is
is irrational and + and , are rational, then
another root is 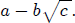
(Like complex roots, irrational real roots appear in conjugate pairs, but only
when the polynomial
has rational coefficients.)
17. Descartes's Rule of Signs Lemma 1.
If p(x) has real coefficients, and if
p(a) = 0 wherea > 0
thenp(x) has at least one more sign
variation than the quotient polynomial q(x)
has sign variations where 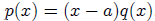
[When the difference in the number of sign variations is greater than 1, the
difference is always
an odd number.]
18. Descartes's Rule of Signs Lemma 2.
If p(x) has real coefficients, the number of
positive zeros of p(x) is not greater than the
number of variations in sign of the coefficients of
p(x)
19. Descartes's Rule of Signs Lemma 3.
Let 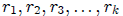 denote 5 positive numbers and let
denote 5 positive numbers and let
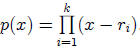
Then the coefficients of p(x) are all
alternating in sign and this polynomial has exactly 5 sign
variations in its coefficients.
20. Descartes's Rule of Signs Lemma 4.
The number of variations in sign of a polynomial with real coefficients is
even if the first and last
coefficients have the same sign, and is odd if the first and last coefficients
have opposite signs.
21. Descartes's Rule of Signs Lemma 5.
If the number of positive zeros of p(x) with
real coefficients is less than the number of sign
variations in p(x) it is less by an even number.
22. Descartes's Rule of Signs Lemma 6.
Each negative root of p(x) corresponds to a
positive root of p(-x) That is, if
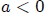
and + is a zero of p(x) then
-a is a positive zero of
p(-x)
23. Descartes's Rule of Signs
Let p(x) be any polynomial with real
coefficients.
(Positive Roots) The number of positive roots of
p(x) = 0 is either equal to the
number of sign variations in the coefficients of
p(x) or else is less than this
number by an even integer.
(Negative Roots) The number of negative roots of
p(x) = 0 is either equal to the
number of sign variations in the coefficients of
p(-x) or else is less than
this number by an even integer.
Note that when determining sign variations we can ignore terms with zero
coefficients.
24. Lemma On Continuous Functions.
Letf(x) and
g(x) be two continuous real-valued functions with
a common domain that is
an open interval (a,b), Furthermore let
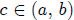 and assume that except when
x = c we have
and assume that except when
x = c we have
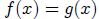 for all
for all 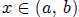 Then we must also have
Then we must also have 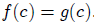
25. Theorem On the Equality of Polynomials
Let 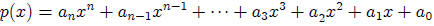 and let
and let
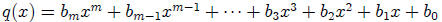 be any two real polynomials of
be any two real polynomials of
degrees n and m respectively. If for all real numbers B,
p(x) = q(x) then
1) m=n
and 2) for all i, if 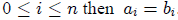
26. Theorem Euclidean Algorithm for Polynomials
Let p(x) and
q(x) be any two polynomials with degrees
≥1. Then there exists a polynomial
d(x)
such that d(x) divides evenly into both
p(x) and q(x).
Moreover, d(x) is such that if
a(x) is any
other common divisor of p(x) and
q(x), then a(x)
divides evenly into d(x). The polynomial
d(x) is
called the Greatest Common Divisor of p(x) and
q(x) is sometimes denoted by
GCD(p(x),q(x))
Except for constant multiples , d(x) is unique.
27. Corollary to the Euclidean Algorithm for
Polynomials
The 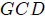 of any two polynomials
p(x) and q(x)
may be expressed as a linear combination of p (x)
of any two polynomials
p(x) and q(x)
may be expressed as a linear combination of p (x)
and q(x)
28. Lemma 1 for Partial Fractions
If 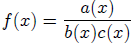 where
where
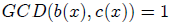 then there exist polynomials
d(x) and e(x)
such
then there exist polynomials
d(x) and e(x)
such
that
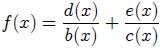
29. Lemma 2 for Partial Fractions
If 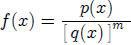 then there exists a polynomial
g(x) and for
then there exists a polynomial
g(x) and for 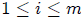 there exist polynomials
there exist polynomials
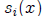 each with degree less than
q(x) such that
each with degree less than
q(x) such that
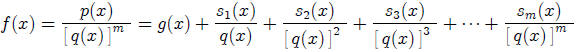
30. Partial Fraction Decomposition Theorem
Let 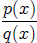 be a rational function where
p(x) and q(x)
are polynomials such that the degree of p(x)
be a rational function where
p(x) and q(x)
are polynomials such that the degree of p(x)
is less than the degree of q(x) Then there exist
algebraic fractions 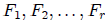 such that
such that
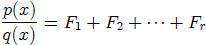 and where each fraction is one of two forms:
and where each fraction is one of two forms:
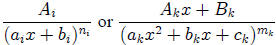 where ,
where ,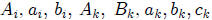 ,
are all real numbers and
,
are all real numbers and
the 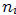 and the
and the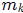 are positive integers and each quadratic expression
are positive integers and each quadratic expression
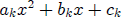 has a
has a
negative
discriminant.
31. Partial Fraction Decomposition Coefficient Theorem
Let 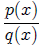 be a rational function where
p(x) and q(x) are polynomials such that the degree of
p(x)
be a rational function where
p(x) and q(x) are polynomials such that the degree of
p(x)
is less than the degree of q(x). If
x = a is a root of
q(x) = 0 of multiplicity ", then in the partial
fraction decomposition of 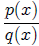 which contains a
term of the form
which contains a
term of the form 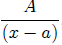 , the constant
, the constant
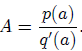
Detailed proofs of all the above theorems may be found on
the author's web site:
homepage.smc.edu\kennedy_john
in a 31-page paper titled Some Polynomial Theorems. See the section on the
author's web site that is
titled Downloadable Papers.
| Prev | Next |