Exponents and Radicals
Radicals and Properties of Radicals
Radicals (or roots) are, in effect, the opposite of exponents. In other
words, the nth root of a number a is a
number b such that
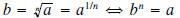
The number b is called an nth root of a. The number n is referred to as the
index of the radical (if no index
appears, n is understood to be 2). The principal nth root of a number is the nth
root of a which has the same
sign as a . For example both 2 and - 2 satisfy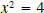 
, but 2 is the (principal)
square root of 4.
Examples:
• 
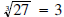since
•
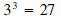
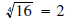since
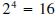(Note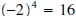 
also, but 2 is the principal 4th root
•
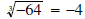since
•
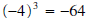
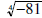is not a real number and we will say that it does not exist. (In this
course we won’t learn how to
take an eventh power of a negative number .)
Radicals are used to define rational exponents :
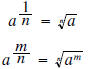
The notation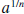 
is extremely useful, and we encourage you to use it whenever
you have to simplify
expressions involving radicals.
Examples:
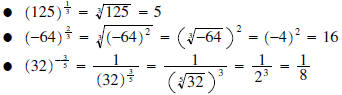
Since radicals are nothing more than rational exponents ,
many of the properties of exponents also apply to
radicals.
| Property | Example |
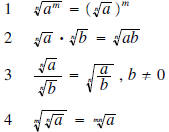 5a If n is odd 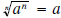 5b If n is even  |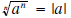
 |
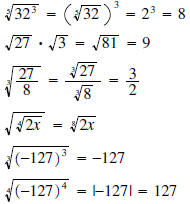The following list is a restatement of these properties,
but in exponential notation . You need to be familiar
with both radical and exponential notation, and be able to convert between the
two.
| Property | Example |
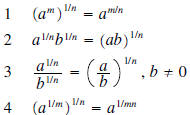 5a If n is odd 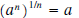 5b If n is even  |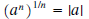
 |
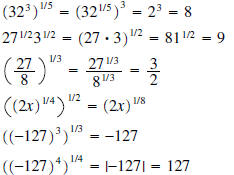Examples:
• 
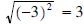(refer to Property 5b)
• 
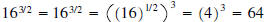(refer to property 1-given the right hand
side)
• 
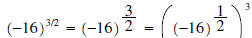(refer to property
1)
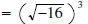
There is no answer as we cannot take the square root of -16.
•
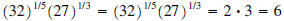
| Prev | Next |