Factoring
• Factoring out a Common Factor : The first
step in factoring any polynomial is to
look for anything that all the terms have in common and then factor it out using
the
distributive property .
Example: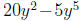 
Here, the terms share the common
factor 5y2 (i.e. 5 is the largest
number that divides both 20 and 5, and both terms contain the variable y with 2
being
the smallest exponent ). So we factor it out:
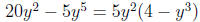
•Factoring by Grouping: Factoring by grouping is useful when we encounter
a polynomial
with more than 3 terms.
Example: 
1. First, we group together terms that share a common factor.
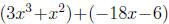
The first group shares an x2 and the second shares a -6.
2. Factor out the common factor from each grouping. You should have left the
same
expression in each group .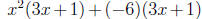 
Here that expression is 3x+1
3. Now factor out that expression.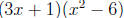 
• Factoring Trinomials - Reverse FOIL: There two basic cases that we’ll
encounter:
1. The leading coefficient is a 1. This is the easier of the two cases: x2 + bx
+ c All
we need to do here is find two numbers whose product is c and sum is b
Example: x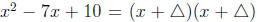
We need to find two numbers that
multiply to give us +10, but add to give us -7. Well, -5 and -2 do the trick. So
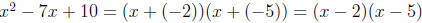
2. The leading coefficient is not a 1. Things are a little trickier here, but
not much.
Again, it’s just FOIL in reverse.
Example: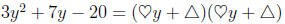 
We need two numbers to fill in for the hearts that will multiply to 3. How about
3 and 1?
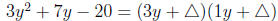
Now we need two numbers to fill in for the triangles that will multiply to -20
AND when we do the INNERS and OUTERS we get 7y. We’ll use the GUESS
and CHECK method to find the two numbers we need.
Let’s try 10 and -2 first:
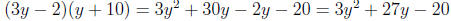
That’s not it! Maybe 5 and -4?
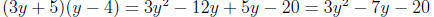
Close, but the sign on the 7 is wrong . Easy to fix - just switch the signs on
the 5
and 4:
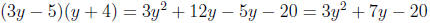Presto !!
• Special Factorizations: Some polynomials are easy to factor because they
fit a
certain mold.
– Difference of Squares :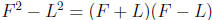
Example: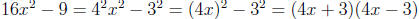
– Perfect Squares : These are polynomials that
factor into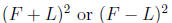 
The pattern we’re looking for here is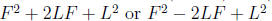 
Example: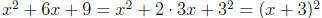 
Example: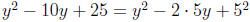 
– Difference of Cubes :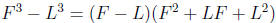
Example: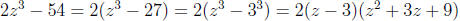 
– Sum of Cubes :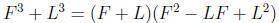 
)
Example: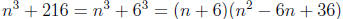 
•Strategy for Factoring:
1. Always factor out the largest common factor first. This will make life easier
for
any further factoring that may need to be done.
2. Look at the number of terms
– Two terms: Is it a difference of squares, difference of cubes or sum of cubes?
– Three terms: Is it a perfect square? Try reverse FOIL.
– Four or more terms: Try factoring by grouping.
3. Always make sure the polynomial is factored COMPLETELY.
| Prev | Next |