Math 50 Exam 1
There are two parts to this exam. The first part consists of 55
problems, including 18 true-false, and calculators are not
allowed . The second part consists of 9 problems and calculators
are allowed. When you are finished with the first part of the exam,
turn it in and get the second part of the exam. Do not take out your
calculators until you turn in part 1 of the exam.
The instruction “Evaluate” means to do the indicated operations
(add, subtract, multiply, divide, etc) and write the expression as a
single number in simplest form . Units are important. That is, 25 is
not a full credit answer when the answer is correctly stated as 25
degrees or 25 feet.
When you are finished with the exam, turn in the exam, answer
sheet and scratch paper.
1. I have read and understand the instructions to this exam.
2. I have read and understand the syllabus.
Part 1 (No Calculator)
A calculator is not allowed on this portion of the exam. When you are
finished with this
part of the exam, turn it in and get the second part of the exam. The
instruction
“Evaluate” means to do the indicated operations (add, subtract, multiply,
divide, etc) and
write the expression as a single number in simplest form. Units are important.
That is, 25
is not a full credit answer when the answer is correctly stated as 25 degrees or
25 feet.
1. Place the correct symbol (<, >, or =) between the two numbers. 16__12
2. Use the roster notation to write the set of negative integers greater than 5.
3. Find the opposite of -40
4. Evaluate -|-7|
5. Evaluate: 16 + (-22) + 5 + (-7)
6. Evaluate: -17 - 33 - (-62) - 24
7. Evaluate -6(2)(-3)
8. Evaluate -7(0)(-5)
9. Evaluate 192 / (-12)
10. Evaluate 16 / 0
11. Find the temperature after a drop of 9 degrees from –2 degrees
12. State the property that justifies the statement: (-3 + 7) + 5 = -3 + (7 + 5)
13. Evaluate 0 / (-8)
14. Write 0.03% as a decimal number.
15. Evaluate (write as a fraction):
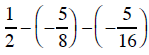
16. Evaluate
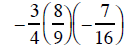
17. Evaluate
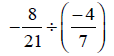
18. Evaluate
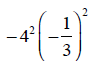
19. Evaluate (write as a fraction)
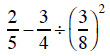
20. Evaluate -a^2 when a = -3.
21. Evaluate 3(a - c) - 2ab when a = 2, b = 3, and c = - 4 .
22. Simplify 8y - 7x + 11x -17y
23. Simplify
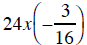
24. Simplify 2(-2x - 7) - (-3 + 5x)
25. Simplify -5x + 4[x - (2 - 7x)] + (-9x)
26. Solve
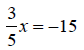
27. Solve x - 4 = -9
28. Solve 13- 9x = -14
29. Solve 5x - 8 = 12x + 13
30. Solve 8x - 3(4x - 5) = -2x - 11
31. Solve
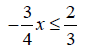
32. Solve 3x - 4 > 5x + 2
33. Translate into a variable expression : “the difference between the square
of x and
twice the total of 7 and x.”
34. Translate into a variable expression: “the quotient of thirty seven and
the difference
between twice a number and eight.”
35. The dividend of a stock is one- eleventh of the price of a stock. Express
the
dividend paid on a stock in terms of the price of the stock.
36. A coin bank contains 22 coins in dimes and quarters. Use one variable to
write
expressions for the number of dimes and the number of quarters in the bank.
37-55. Circle True if the statement is always true, otherwise circle False.
| 37. | True | False | The Commutative Property of Addition states a + b = b + a |
| 38. | True | False | True False In the expression 8y^3 - 4y , the terms are 8y^3 and 4y. |
| 39. | True | False | If the sum of two numbers is 12 and one of the numbers is x, then
the other number can be expressed as x – 12. |
| 40. | True | False | -5^2 is read “negative five squared.” |
| 41. | True | False | Terms are addends. |
| 42. | True | False |
 |
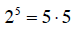| 43. | True | False | Like Terms of an expression are terms that have identical variable parts. |
| 44. | True | False | Constant terms are always like terms |
| 45. | True | False | If x is an integer, then |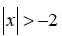
| 46. | True | False | If x is an integer, then |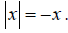
| 47. | True | False | If x is a negative integer, then |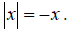
| 48. | True | False | If a and b are integers and a < b, then |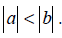
| 49. | True | False | To find the opposite of any integer, multiply the integer by -1. |
| 50. | True | False | To find the opposite of any integer, divide the integer by -1. |
| 51. | True | False | If a and b are integers and b = 0 then a/b = 0 . |
| 52. | True | False | The number π/3 is an example of a rational number |
| 53. | True | False | -12 is an example of a number that is both a
rational number and an integer. |
| 54. | True | False |  |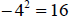
| 55. | True | False | The product of a number and its multiplicative inverse is one |
Part 2 – You may use a calculator.
The instruction “Evaluate” means to do the indicated
operation (add, subtract, multiply,
divide, etc) and write the expression as a single number in simplest form. Units
are
important. That is, 25 is not a full credit answer when the answer is correctly
stated as 25
degrees or 25 feet. Make sure you show your work on problems 6-9.
1. Write 11/30 as a decimal number. Place a bar over any repeating part.
2. Write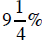
as a fraction.
3. Write 11/18 as a percent. Round to the nearest tenth of a percent.
4. Evaluate 1.75 - (-4.67)+ 0.24
5. Evaluate -39.44 /(-3.4)
6. Palmer’s average running speed is 3 kilometers per hour
faster that his walking
speed. If Palmer can run a 30 km in 2 hours, how long would it take him to walk
the
same course?
7. Karen invests $1200 in a simple interest account and
earns $72 in 8 months. What
is the annual simple interest rate?
8. A pharmacist has 50 g of a cream that contains 75%
glycerin. How many grams of
the cream are not glycerin?
9. A lever is 25 feet long. At a distance of 12 feet from
the fulcrum, a force of 26 lb is
applied. How large a force must be applied tot he other end of the lever so that
the
system will balance?
| Prev | Next |