Finding Least Common Denominators
Objectives:
1. The teacher will explore using Cuisenaire Rods to determine the Least common
Denominator of two unlike fractions.
_______________________________________________________________________
TOPIC: FINDING THE LEAST COMMON DENOMINATOR [FINDING
LCMs]
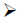 Materials: CUISENAIRE RODS
Materials: CUISENAIRE RODS
1. As a group , use Cuisenaire Rods and work through these steps to find the LCM (6, 8).
Our Goal:
We wish to find the LCM (6, 8). We need to find a Cuisenaire Rod train that is:
i. A multiple of 6
ii . A multiple of 8
Iii. The smallest (shortest) train that will work.
It turns out that finding the LCM is extremely easy to model with Cuisenaire Rods using the numbering with the white rod as 1:
a. If the Dark Green Rod is 6, then all trains made of
Dark Green Rods represent numbers that are :
____________________ of 6
Starting Sketch:
b. If the Brown Rod is 8, then all trains made of Brown
Rods represent numbers that are :
____________________ of 8
Starting Sketch:
c. If the Dark Green Rod is 6 and the Brown Rod is 8, then ALL same-length trains that can be made of all Dark Green OR all Brown Rods represent numbers that are :
Starting Sketch:
d. If the Dark Green Rod is 6 and the Brown Rod is 8, then THE SHORTEST same-length trains that can be made of all Dark Green OR all Brown Rods represent the number that is :
Sketch:
e. This train is _____ whites long, therefore _____ is the
LCM of 6 and 8.
At this point you should have trains that look like this on your table .
| DARK | GREEN | RODS | DG | ||
| BROWN | RODS | BR | |||
• Since the white rod is 1, these trains are both 24 whites long and they both represent 24 = LCM (6, 8)
2. As a group , use Cuisenaire Rods and determine the LCM (16, 24). Step out your work and draw well -labeled sketches. What’s One?
3. Suppose that you wish to explain how to find the LEAST COMMON MULTIPLE of two numbers to a student. Using the above steps as a general guide, explain how you would share finding the LCM(4, 6) with a student. Discuss this with your group members and show all of the (completed) steps here.
| Prev | Next |