Quadratic Equations

This section contains one mathematical example : Al Khwarizmi's solution to the quadratic equation
x^2 +10x = 39: Recall that we already knew that ancient people knew how to solve quadratic equations.
(We have seen this particular equation more than once already.) We have also seen multiple
examples in which a mathematician used the method of completing the square (as Al Khwarizmi
does). So what is supposed to be new here?
ANSWER: Al Khwarizmi's geometric justification for his methods. The approach which is a real
mix of algebra and geometry is unfamiliar to modern algebra students and (in my opinion) quite
interesting.

Here are some questions we should address:
1. Can we write out the argument given in the book in a more general form? What are his
underlying assumptions and why does he make them?
2. Where does Al Khwarizmi's work fit historically? What of his work is original? What isn't?

From the Book

(a general version of) Al Khwarizmi's argument that the solution of

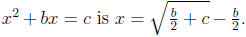
Some Historical Context

A. The Babylonians
There are many many examples in Babylonian texts of solutions to quadratic equations . One standard type of example was to find the length and width of a rectangle given its area and semiperimeter.

1. (From tablet YBC4663 [Katz pg 23]) Find the length and width of a rectangle with semiperimeter 6 1/2 and area 7 1/2.

The scribe's solution was to halve 6 1/2 to get 3 1/4. Now square 3 1/4 to get 10 9/16. From this
is subtracted 7 1/2, leaving 3 1/16, and then the square root is extracted to get 1 3/4. The length
is thus 3 1/4 + 1 3/4 = 5 and the width is given as 3 1/4 - 1 3/4=1 1/2.

2. There are examples of specific quadratic equations of the form x^2+bx = c where the scribe gives
directions equivalent to completing the square just as in the example in the text.

3. (From tablet MB 13901 [Katz pg 25]) The problem in modern notation is 11x^2 +7x = 61=4: The
solution is to multiply the whole equation by 11 so that a substitution of y = 11x is a quadratic
with coefficient 1 for the y ^2 term :

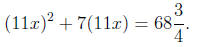
Then the scribe completes the square to get:

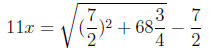
and then (he would normally) divide by 11 to get x ... except in this case he noted that the reciprocal
of 11 "cannot be solved." Nevertheless, he gave the answer that the unknown side was 1/2,
presumably because the example was simple and manufactured for an easy answer.

Summary : The examples are all specific. There are lots of examples but they are not organized
according to some classification scheme. Some of the language suggests the scribes thought about
these problems geometrically but there are no diagrams. There are not attempts to show that a
particular technique is truly general.

B. Euclid's Elements: Book II (geometric algebra)

definition: Any rectangle is said to be contained by the two straight lines forming the right angle.

Proposition II-6: If a straight line is bisected and a straight line is added to it , the rectangle
contained by the whole with the added straight line and the added straight line together with the
square on the half is equal to the square on the straight line made up of the half and the added
straight line.

Proposition II-11: To cut a given straight line so that the rectangle contained by the whole
and one of the segments is equal to the square on the remaining segment. (ie Euclid constructs a
solution to the equation: x^2 + a^2 = ax:)

Summary: Euclid had the quadratic formula (or his various versions of it) with proofs of their
correctness, but all in a purely geometric form.