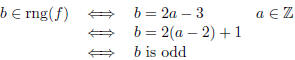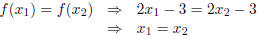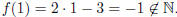| |
Introduction
You’ve already encountered functions throughout your education.
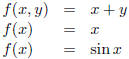
Here, however, we will study functions on discrete
domains and
ranges. Moreover, we generalize functions to mappings. Thus,
there may not always be a “nice” way of writing functions like
above. |
Definition
Function
Definition
A function f from a set A to a set B is an assignment of exactly
one element of B to each element of A. We write f(a) = b if b is
the unique element of B assigned by the function f to the
element
a ∈ A. If f is a function from A to B, we write
f : A → B
This can be read as “f maps A to B”. |
Note the subtlety:
 Each and every element in A
has a single mapping. Each and every element in A
has a single mapping.
 Each element in B may be
mapped to by several elements in Each element in B may be
mapped to by several elements in
A or not at all. |
Definitions
Terminology
Definition
Let f : A → B and let f(a) = b. Then we use the following
terminology :
 A is the domain of f,
denoted dom(f). A is the domain of f,
denoted dom(f).
 B is the codomain of
f. B is the codomain of
f.
 b is the image of a. b is the image of a.
 a is the preimage of b . a is the preimage of b .
 The range of f is the
set of all images of elements of A, The range of f is the
set of all images of elements of A,
denoted rng(f). |
|
Definitions
Visualization
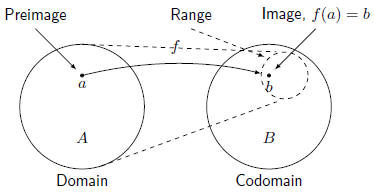
A function, f : A → B. |
Definition I
More Definitions
Definition
Let f1 and f2 be functions from a set A to R. Then f1 + f2 and
f1f2 are also functions from A to R defined by

|
| Example |
|
Definition II
More Definitions
|
Definition III
More Definitions
Note that here, an image is a set rather than an element.
|
Definition IV
More Definitions
A function f whose domain and codomain
are subsets of the set of
real numbers is called strictly increasing if f(x) < f(y)
whenever
x < y and x and y are in the domain of f. A function f is called
strictly decreasing if f(x) > f(y) whenever x < y and x and y
are
in the domain of f. |
|
Injections, Surjections, Bijections I
Definitions
Definition
A function f is said to be one-to-one (or injective) if

for all x and y in the domain of f. A function is an injection
if it is
one-to-one |
Intuitively, an injection simply means that each
element in A
uniquely maps to an element in b.
It may be useful to think of the contrapositive of this definition:
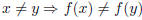
|
Injections, Surjections, Bijections II
Definitions
Definition
A function f : A → B is called onto (or surjective) if for every
element b ∈ B there is an element a ∈ A with f(a) = b. A
function is called a surjection if it is onto. |
Again, intuitively, a surjection means that every
element in the
codomain is mapped. This implies that the range is the same as
the codomain. |
Injections, Surjections, Bijections III
Definitions
Definition
A function f is a one-to-one correspondence (or a bijection, if
it is
both one-to-one and onto. |
One-to-one correspondences are important because
they endow a
function with an inverse. They also allow us to have a concept of
cardinality for infinite sets!
Let’s take a look at a few general examples to get the feel for
these definitions. |
Function Examples
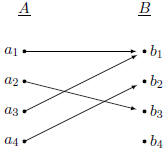
A Non-function
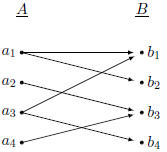
This is not a function: Both
 and and
 map to more
than one map to more
than one
element in B. |
Function Examples
A Function; Neither One-To-One Nor Onto
This function not one-to-one since
 and and
 both
map to both
map to 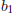 . It is . It is
not onto either since 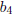 is not mapped to by any element in A. is not mapped to by any element in A. |
Function Examples
One-To-One, Not Onto

This function is one-to-one since every
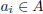 maps to a unique
maps to a unique
element in B. However, it is not onto since
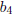 is not mapped to by is not mapped to by
any element in A. |
Function Examples
Onto, Not One-To-One
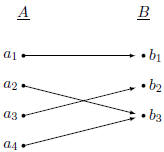
This function is onto since every element
 is mapped to by
is mapped to by
some element in A. However, it is not one-to-one since
 is is
mapped to more than one element in A. |
Function Examples
A Bijection
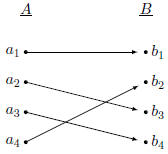
This function is a bijection because it is both
one-to-one and onto;
every element in A maps to a unique element in B and every
element in B is mapped by some element in A. |
Exercises I
Exercise I
Example
Let f : Z → Z be defined by
f(x) = 2x - 3
What is the domain and range of f? Is it onto? One-to-one? |
Clearly, dom(f) = Z. To see what the range is,
note that
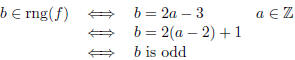
|
Exercises II
Exercise I
Therefore, the range is the set of all odd integers. Since the range
and codomain are different , (i.e. rng(f) ≠ Z) we can also
conclude that f is not onto.
However, f is one-to-one. To prove this, note that
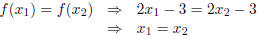
follows from simple algebra . |
Exercises
Exercise II
Example
Let f be as before,
f(x) = 2x - 3
but now define f : N → N. What is the domain and range of f? Is
it onto? One-to-one? |
By changing the domain /codomain in this example, f
is not even a
function anymore. Consider 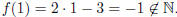 |
 Each and every element in A
has a single mapping.
Each and every element in A
has a single mapping.

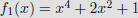 and
and
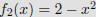 then
then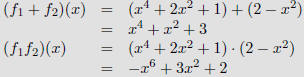
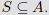 The image of S is the subset of B
The image of S is the subset of B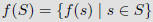

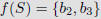

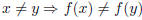

 and
and
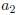 map to more
than one
map to more
than one
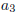 both
map to
both
map to 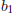 . It is
. It is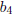 is not mapped to by any element in A.
is not mapped to by any element in A.
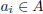 maps to a unique
maps to a unique
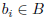 is mapped to by
is mapped to by is
is