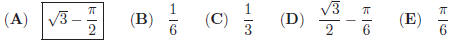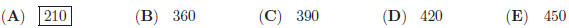MATH DIVISION I COMPREHENSIVE EXAM
16. If the height of a cylinder is increased by 1/9, and
the radius of the cylinder is decreased by 1/10,
what will happen to the volume of the cylinder ?
(A) Same as the volume of the original cylinder
(B) Increases by 1/9
(C) Decreases by 1/9
(D) Increases by 1/10
|
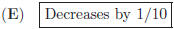
17. Let the radii of the three semicircles all be R, their centers A, B, C are in a common line, and the circle with center D has only one point in common with the given semicircles re- spectively. Suppose the radius of the circle with center D is r, then R : r =?  |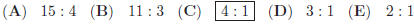
 |
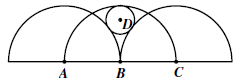18. In the figure shown, find CD? |
 |
|
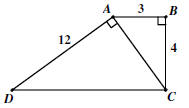19. Three circles of radius 1 are mutually tangent as shown. What is the area of the gap they enclose?
|
 |
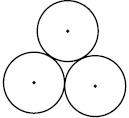20. Find the difference of the maximum value and the
minimum value of the function:
3 sin x + 4 cos x + 5.
21. If real numbers x, y satisfy
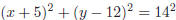, then the minimum value of
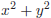equals ?
(E) Cannot be determined
22. Find the maximum value of k which ensures that the
inequality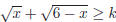 
has a solution
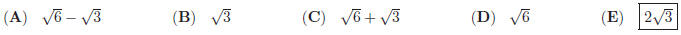
23. How many of the solutions to the following equation are negative?
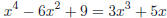
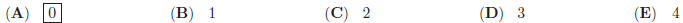
24. Jack and Jim start at the same time to ride from place
A to place B, 60 miles away. Jack travels 4
miles an hour slower than Jim. Jim reaches B and at once turns back meeting Jack
12 miles from B.
The rate of Jack was:
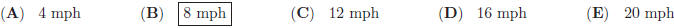
25. From a group of boys and girls, 15 girls leave. There
are then left two boys for each girl. After 45
boys leave, there are then 5 girls for each boy. The number of girls in the
beginning was:
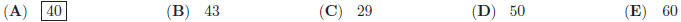
26. For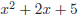 
to be a factor
of
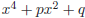, the value of q must be
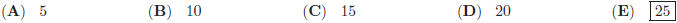
27. Let a and b be positive numbers not equal to 1,
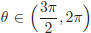. If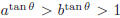 
,
then which of
the following inequalities is true ?
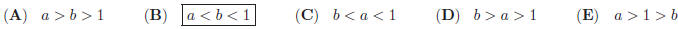
28. How many pairs of integers (x, y) satisfying the
function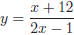 
?
(E) Infinite
29. Let f(x) be a polynomial of degree 2007 satisfying
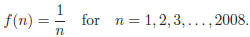
What is the value of f(2009)?
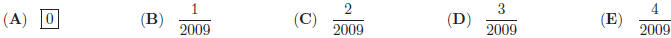
30. It rained on exactly 11 days during Jane's holiday
trip. On each rainy day it rained either in the
morning or in the afternoon but not both. There are exactly 13 afternoons when
it did not rain and
exactly 16 mornings when it did not rain. How many days did the trip last?
31. Let a, b, c, d be positive real numbers with a < b < c
< d. Given that a, b, c, d are the first four
terms in an arithmetic sequence , and a, b, d are the first three terms in a
geometric sequence, what
is the value of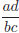 
?
32. A right triangle with integer side lengths a, b and c
satisfies a < b < c and a + c = 49. What is the
area of the right triangle?
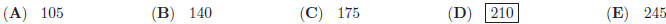
33. In a triangle ABC,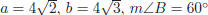
,then
m∠A =?
34. Suppose ! is a complex number satisfying
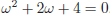.then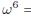 
35. If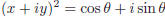 
, find the
absolute value of y, given that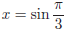 
and
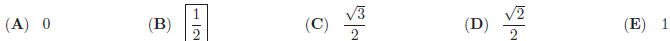
36. Let S be the sum of the first 10 terms of the
sequence:
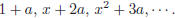Then S =?
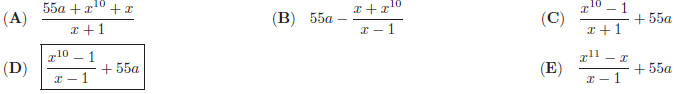
37. Given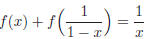 
where x ≠ 0,
1, find the value of f(2).
(E) Cannot be determined
38. How many points do the graphs of
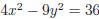and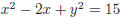 
have
in common?
|
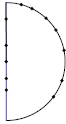
39. Twelve points are arranged on a semicircle as shown in the diagram.
How many triangles can we draw from the given points?
|
 |
40. Suppose y is the determinant of the matrix
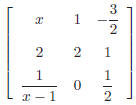
Then what is the minimum value of y given x > 1?
41. Suppose that a is a non- zero real number for which sin
x + sin y = a and cos x + cos y = 2a. What is
the value of cos(x - y) ?
42. Suppose that f(x) = ax + b where a and b are real
numbers. Given that f(f(f(x))) = 8x + 21, what
is the value of a + b ?
43. If sin x = 2 cos x, then what is the value of sin x cos x ?
44. Which of the numbers below is a solution to the following equation ?
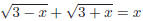
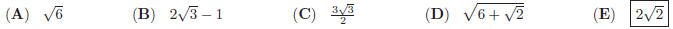
45. What is the value of the following product ?
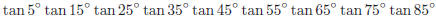
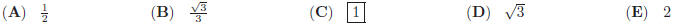
46. How many positive real numbers x are solutions to the
equation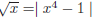 
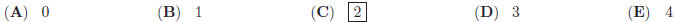
47. Order sin 1, sin 2, sin 3 from smallest to largest (the angles are measured in radians).
48. The line y = 3 - x intersects the parabola y = 3x - x2
in two points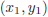 
and
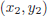. What is
?
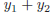49. Given that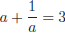 
, what is
the value of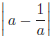 
50. A box of coins contains a total of 26.00 in nickels,
dimes, and quarters. If there is the same number
of nickels as dimes, but twice as many quarters as nickels, how many dimes are
in the box?
| Prev | Next |