Integrals of Rational Functions

1 Overview

A rational function has the form

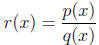
where p and q are polynomials. For example,

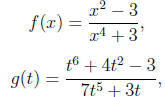
and

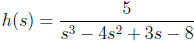
are all rational functions. A rational function is called proper if the degree of the numerator
is less than the degree of the denominator, and improper otherwise. Thus, f and h are proper
rational functions, while g is an improper rational function.

Indefinite integrals (antiderivatives) of rational functions can always be found by the
following steps:

1. Polynomial Division: Divide the denominator into the numerator (if needed) to write
the integrand as a polynomial plus a proper rational function.

2. Partial Fraction Expansion : Expand the proper rational function using partial fractions.

3. Completing the Square : If any terms involve quadratics, eliminate the linear term if
needed by completing the square.

4. Term by Term Integration: Use elementary integral formulas and substitution .

Before detailing this general approach, we will first look at some simple cases where ordinary
substitution works easily. Then we will look at each of the above steps in turn, and finally
put them together to find integrals of rational functions.

Note: While this handout is concerned primarily with integrating rational functions,
many of the techniques discussed here are useful in other contexts. In particular, partial
fraction expansions are used extensively in solving differential equations by Laplace transform
methods.

2 Substitution

In some special cases, integrals (antiderivatives) of rational functions can be found by simple
substitutions. The easiest case is when the numerator is the derivative of the denominator
(or differs by a multiplicative constant ).

Example 1: Find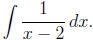

Solution: Here we use the substitution

w = x − 2,

from which we compute

dw = dx.

Making this substitution then gives

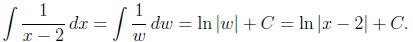
Example 2: Find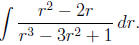 

Solution: Here we notice that the numerator is the derivative of the denominator (to within
a constant factor). Therefore, we substitute for the denominator

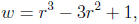
which implies

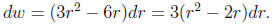
Making this substitution gives

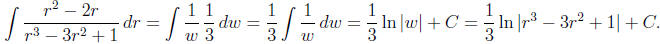
Sometimes a substitution can be helpful even though the numerator isn’t the derivative
of the denominator.

Example 3: Find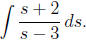

Solution: Here we can substitute for the denominator, choosing w = s − 3, which implies
dw = ds. Since we must convert everything to w, including the numerator, we solve for s to
obtain s = w + 3 and thus s + 2 = w + 5. Making these substitutions gives

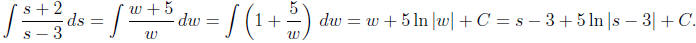
3 Polynomial Division

When no simple substitution works for integrating a given rational function, the systematic
approach is to use partial fraction expansions. Since this technique works for proper rational
functions, if the integrand is an improper rational function we must first express it as a
polynomial plus a proper rational function. That is, if we want to integrate p(x)/q(x) and
the degree of the numerator p is not less than the degree of the denominator q, our first step
is to write

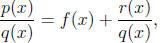
where f is a polynomial and the degree of the remainder r is less than the degree of q. How
do we find f and r? Long division will always work.

Example 4: Express 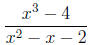as a polynomial plus a proper rational function.

Solution: Using long division, just like for numbers (don’t forget the zeros for the “missing”
powers of x ) we find:

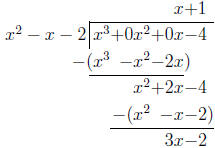
Thus we can write

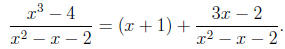
Sometimes it isn’t necessary to do the long division so formally, as long as we can arrive
at the proper form.

Example 5: Express 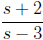as a polynomial plus a proper rational function.

Solution: By adding and subtracting in the numerator we can simplify this rational function
as follows:

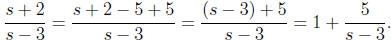
Note that if we integrate this result, we obtain s + 5 ln |s − 3| + C. Compare this with the
result of Example 3: can you explain why both answers are correct?

4 Partial Fraction Expansion

The idea of partial fraction expansion is to take a proper rational function and express it
as the sum of simpler rational functions. This is just the reverse of ordinary addition of
rationals. For example, we know that

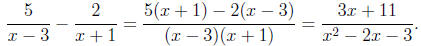
What we want to do now is turn this around: that is, start with the right-hand side of this
equation (a proper rational function) and somehow split it up to obtain the left-hand side
(a sum of simpler rational functions). This can be accomplished step by step as follows.

Step 1: Factor the denominator. In the simplest case, we can factor the denominator
into linear (degree one) factors. For instance, for the above example we have by inspection
that

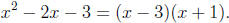
In cases which can’t be factored readily, we can turn to the quadratic formula (for quadratics)
or other root -finding methods for higher-degree polynomials, as studied in high school
algebra. Sometimes a quadratic (degree two) factor cannot be further broken down (using
real numbers): x² + 4 is such an irreducible quadratic. However, it can be shown that any
polynomial with real coefficients is a product of linear and/or irreducible quadratic factors
with real coefficients.

Step 2: Expand using undetermined coefficients A, B, C, . . . . This means
writing out the rational function as a sum of terms involving the factors of the denominator.
For the example at hand, this expansion takes the form

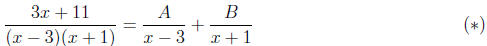
where A and B are constants which are yet to be determined. Note: the specific form of the
expansion depends on what type of factors the denominator has—more on this a bit later.

Step 3: Clear fractions. Multiply both sides by the denominator so no fractions
remain. For the example at hand, we multiply both sides of equation (*) by (x − 3)(x + 1)
to obtain

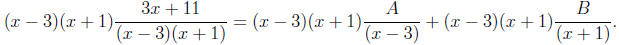
Cancelling the common factors reduces this to

3x + 11 = (x + 1)A + (x − 3)B. (** )

Step 4: Solve for the coefficients A, B, C, . . . . There are two approaches here.
The systematic approach is to gather together like powers of the variable and equate their
coefficients, which gives a set of equations to solve for A, B, C, . . . . For the example at
hand, we rewrite the equation (**) as

3x + 11 = (A + B)x + (A − 3B).

Since this must hold for all values of x, the coefficients of like powers of x on both sides must
match. Thus, from the x terms we obtain

3 = A + B,

and from the constant terms we obtain

11 = A − 3B.

Solving these equations yields A = 5 and B = −2.

An alternate (and often easier) approach here is to simply plug specific values of x into
the expansion (after clearing fractions) to obtain equations for A, B, C, . . . . By choosing
the x values intelligently, the resulting equations usually can be made much simpler. For the
example at hand, we can plug x = 3 into equation (**) to obtain

3(3) + 11 = (3 + 1)A + (3 − 3)B,

which simplifies immediately to 20 = 4A so A = 5. Likewise, plugging x = −1 into equation
(**) gives

3(−1) + 11 = (−1 + 1)A + (−1 − 3)B,

which reduces to 8 = −4B so B = −2.

Step 5: Substitute A, B, C, . . . into the expansion. At this point we’re done:
since the values of the coefficients are known, the expansion is known. For the example at
hand, we substitute A = 5 and B = −2 (from step 4) into equation (*) to obtain

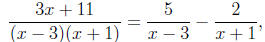
which is the desired partial fraction expansion.

Example 6: Expand 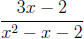using partial fractions.

Solution: First, we factor the denominator:

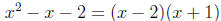
by inspection). Next, we set up the partial fraction expansion:

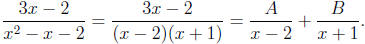
Clearing fractions (by multiplying by the denominator) gives

3x − 2 = (x + 1)A + (x − 2)B.

To solve for the undetermined coefficients A and B we use the second of the two methods
explained in step 4 above (since it is easier). Which values of x should we choose? A natural
choice is x = 2, since when we plug it into the equation the B term will drop out: we get

3(2) − 2 = (2 + 1)A + (2 − 2)B,

which reduces to 4 = 3A so A = 4/3. The other natural choice is x = −1, since it will cause
the A term to drop out: plugging it in gives

3(−1) − 2 = (−1 + 1)A + (−1 − 2)B,

which simplifies to −5 = −3B so B = 5/3. Substituting these values for A and B into the
expansion gives

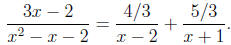
Note that we can easily check this result by combining the terms on the right-hand side.

What form should we assume for the partial fraction expansion in step 2? The correct
form depends on the factors of the denominator as follows:

• For each linear factor in the denominator, use a constant divided by that factor—and
another for each multiple of that factor if it is repeated.

• For each irreducible quadratic factor in the denominator, use a linear term divided by
that factor—and another for each multiple of that factor if it is repeated.

Some examples of the correct forms of expansions should make this clear:

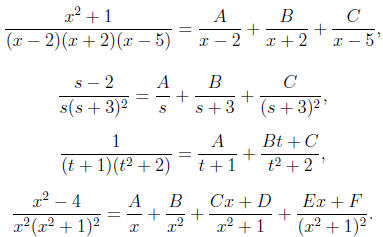
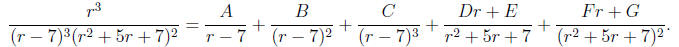
Note that:

• The rational functions on the left-hand side are all proper: if they were not, we must
first divide out the denominator as explained in section 3.

• Some of the coefficients A, B, C, . . . might turn out to be zero, but we cannot assume
that from the start.