Linear Homogeneous Second-Order Ordinary Differential Equations Analysis and Visualization
Linear Homogeneous Second- Order Ordinary Differential Equations Analysis and Visualization
Example
10.6
Show that for all real numbers 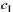 and
and
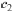
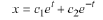
is a solution to the ODE
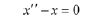
Solution: Calculate
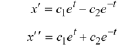
Then
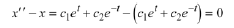
hence 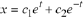 is a solution to the ODE.
is a solution to the ODE.
End of Example 10.6
The last example admits the following generalization.
Theorem
10.7 [Linearity]
If 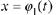 and
and
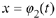 are solutions to Eqn. (10.4)
are solutions to Eqn. (10.4)

then for all real numbers
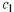 and
and 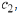 the linear combination
the linear combination
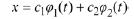
is also a solution.
Definition
10.8 [Characteristic Polynomial]
The polynomial

is called the characteristic polynomial for the homogeneous ODE
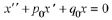
The roots of the characteristic polynomial are called its characteristic roots.
The characteristic roots can be classified into one of three categories:
• Real distinct; i.e.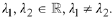
•
Real identical; i.e.,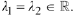
•
Complex conjugate ; i.e.,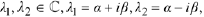 with
with
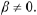
For instance. if 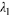 and
and
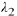 are real distinct, we see that
are real distinct, we see that
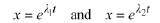
must be solutions to Eqn. (10.4). Even when the roots
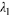 and
and 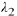 are identical or are
complex conjugate, we will determine
are identical or are
complex conjugate, we will determine
appropriate solutions. The next theorem provides these.
Theorem
10.9 [General Solution]
Suppose the coefficients 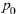 and
and
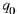 are real numbers and that the characteristic
polynomial
are real numbers and that the characteristic
polynomial 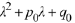 has roots
has roots
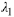
and 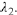 There are three possibilities for a
general solution to
There are three possibilities for a
general solution to 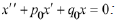
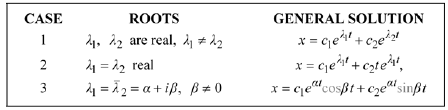
where 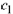 and
and
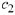 are arbitrary real numbers. Each of these
solutions is defined at for all
are arbitrary real numbers. Each of these
solutions is defined at for all 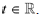
Proof:
Observe that we can set
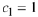 and or and
and or and
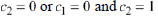 in Example 10.6 to obtain the particular
solutions
in Example 10.6 to obtain the particular
solutions 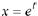 and
and
 In fact, we can do the same in Case 1 of Theorem 10.9 to get the particular
solutions
In fact, we can do the same in Case 1 of Theorem 10.9 to get the particular
solutions 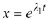 and
and
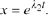 These
These
particular solutions will play an important role in the theory of linear
second -order ODEs with constant coefficients .
Example
10.10:
Determine the general solution to the ODE
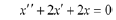
Solution: The characteristic equation is
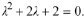 As this polynomial doesn't factor
readily , use the quadratic formula to calculate the
As this polynomial doesn't factor
readily , use the quadratic formula to calculate the
characteristic roots
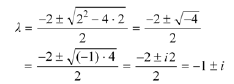
to get complex conjugate roots Note that
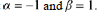 So according to Theorem 10.6, Case
3 prevails so that the general solution is
So according to Theorem 10.6, Case
3 prevails so that the general solution is
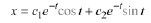
The reader should check this;, i.e., verify that
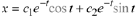 is a solution to the ODE.
is a solution to the ODE.
End
of Example 10.10
Observe that we can set 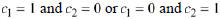 in Example 10.9 to obtain the particular
solutions
in Example 10.9 to obtain the particular
solutions 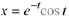
and 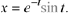 In fact, we can do the same in Case 3 of Theorem 10.9 to get the particular
solutions
In fact, we can do the same in Case 3 of Theorem 10.9 to get the particular
solutions 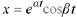 and
and
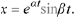 In fact, the particular solutions obtained by setting
In fact, the particular solutions obtained by setting
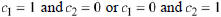 in Theorem 10.6
are
in Theorem 10.6
are
distinguished by the role they play with regard solving an IVP for
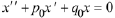
Theorem 10.6 begs the question: Do these cases cover all possible solutions?
Given a set of initial conditions, say 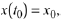
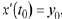 can we be confident that one of the three cases provides a unique solution? The
answer is YES as we shall soon
can we be confident that one of the three cases provides a unique solution? The
answer is YES as we shall soon
see. But first we examine how initial values affect solutions.
10.4 INITIAL CONDITIONS
Whereas a first-order ODE
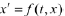 generally admits a single solution that satisfies
generally admits a single solution that satisfies
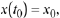 a
second-order ODE can
a
second-order ODE can
have infinitely many solutions satisfying 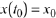 It is instructive to examine a simple
ODE and see why this is so.
It is instructive to examine a simple
ODE and see why this is so.
Consider the ODE

Calculate the characteristic roots by solving the quadratic equation
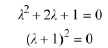
Thus we get the real repeated root
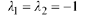
From Case 2 of Theorem 10.9, the general solution is
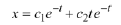
Now suppose we wish to determine the solution that satisfies
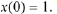 Thus we must have
Thus we must have
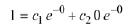
which implies
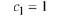
As no restriction is placed on
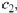 we can only say that the solution is
we can only say that the solution is
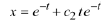
Consequently, there are infinitely many solutions - one for each value of
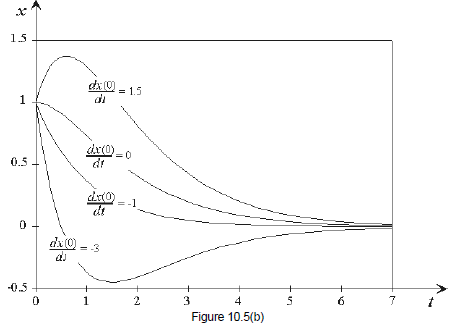
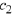 Figure
10.5(a) depicts four such solutions.
Figure
10.5(a) depicts four such solutions.
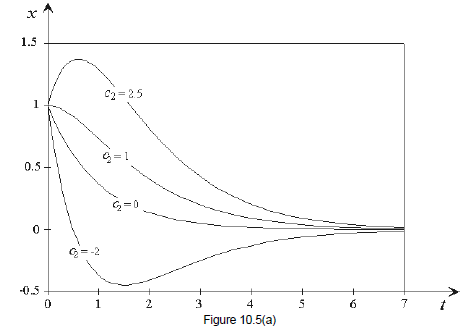
Observe how each of the solutions issues forth from the initial point Each
solution has a different slope at 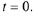 We
We
can calculate these from the corresponding solutions. Since
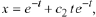 then
then
For each value of 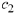 we calculate the corresponding value of
we calculate the corresponding value of
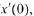 the slope of the
corresponding solution at
the slope of the
corresponding solution at 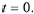 For
For
instance, when 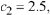
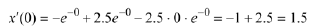
The following table lists these values.
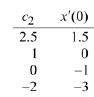
Figure 10.5(b) displays the same graphs , this time labeled with the values of
 instead of
instead of
We see from the preceding analysis of the solutions to
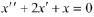 that specification of a
value for
that specification of a
value for 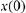 and a value for
and a value for
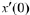 is sufficient to uniquely determine a solution. With this in mind we can define
what we mean by initial conditions and
is sufficient to uniquely determine a solution. With this in mind we can define
what we mean by initial conditions and
an IVP for a linear homogeneous second-order ODE.
Definition 10.11 (Initial Value Problem)
An initial value problem (IVP) for a linear homogeneous second-order ODE
consists of two things :
1. An ODE

and
2. Initial Conditions
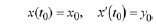
where 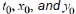 are given numbers and are called initial values or initial data.
are given numbers and are called initial values or initial data.
| Prev | Next |