MATH 360 Review of Set Theory
Definition: A function f : X → Y is a rule that associates for all
x ∈ X exactly
one element of Y . (The actual definition involves relations, so I won't go into
that,
but this will do.)
• The element x maps to its image, f(x) ∈ Y : x → f(x). Note that
the image
of an element is always an element of Y .
• The function f = is called the map
• The set X is the domain
• The set {y ∈ Y : y = f(x) for some x ∈ X} is called the range. Note
that the
range are the elements in Y that are actually mapped to.
• The set Y is the codomain. (Note: in Calculus, the terms ”range” and
”codomain” are used interchangeably. But not here in Topology!)
• Now, let U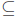 
X. We can map the entire set U
using the map f. This is called
the image of U, and has notation f(U) = {y ∈ Y : y = f(x) for some x ∈
U}.
Note that the image of a set is always a subset of Y .
Examples:
1. Let m : R → R be the function f(x) = x2 + 1. The domain=codomain=R
but
the range is [1,∞). If U = (0,∞), then the image of U is m(U) = (1,∞). If
V = {±2}, then the image of V is m(V ) = {5}. Also, m(2) = 5,m(−2) = 5.
Note that the images of sets are always sets, but that when we map over the
element 2, we get the element 5! (Thus the image of the set N = {2} would be
the set m(N) = {5} ≠ 5!)
2. Let g : R → [−1, 1] by g(x) = sin(x). The domain is R
and the codomain=range=
[-1,1]. Note: the image of the set (0, π/2) is g(0, 2π ) = [−1, 1] still.
3. Let h : R → [−1, 5] be the function given by
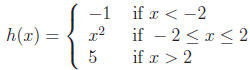
The domain of h is R, the codomain is [-1,5] and the range
is {−1}∪[0, 4]∪{5}.
The image of the element 5 is f(5) = 5. The image of 2 is f(2) = 4. The image
of Z is h(Z) = {−1, 0, 1, 4, 5}.
4. Let q : R → R by q(x) =x2 + 1. Then q([1, 2]) = [2, 5], q([−1, 1]
= [1, 2].
5. Let r : R → R by r(x) = 4−x2. Then r([0, 2]) = [0, 4], r([−2, 2])
= [0, 4], r([2,∞)) =
(−∞, 0].
Theorem: Let f : X → Y be a function and let {Aα : α∈
} be an indexed
collection of subsets of X. Then
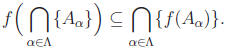
Proof: Let y ∈ f
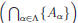. Then there exists x ∈
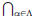{Aα } such that y = f(x).
Since x ∈ 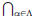{Aα }, it follows that
x ∈ Aα for each α ∈
. Hence f(x) ∈ f(Aα ) for
each α ∈ . Therefore
f(x) ∈
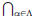{f(Aα )}. Since y = f(x), we are
done.
Note that the other inclusion is not necessarily true: Let f : R → R by f(x) = x2.
Let U = [−2, 0], V = [0, 2]. then f(U ∩ V ) = f({0}) = {0}. However, f(U) ∩ f(V
) =
[0, 4] ∩ [0, 4] = [0, 4]. Thus f(U) ∩ f(V )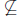 
f(U ∩ V ).
Definition: f : X → Y is one-to-one or injective provided that if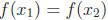 
then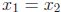 
for all
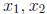∈ X.
Examples:
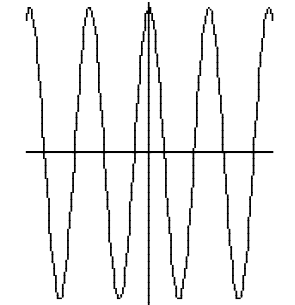
1. The following is a graph of function f : R → R that is not one-to-one. (Why
not?) Note: this function is supposed to keep oscillating forever - at the same
height.
2. Let f : R → R where f(x) = x3 + 1. Is f
one-to-one? To prove it, we assume
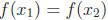, for
∈ R. Then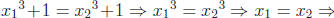 
f is one-to-one.
3. Is the function g (from the previous page ) one-to-one? How about h?
Definition: The function f : X → Y is onto or surjective provided
that for each
y ∈ Y there is at least one x ∈ X such that f(x) = y.
Examples:
1. The following is a graph of function f : R → R that is not onto. (Why?) How
could we change the codomain so that the function would be onto?
2. Is g onto? Yes - every real number y with −1 ≤ y ≤ 1 is
mapped to by some x.
Let x = arcsin(y). Then g(x) = sin(arcsin(y)) = y.
3. How about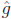 
: R → R given by
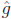(x) = sin(x)? No. For example, let y = 10.
There is no x ∈ R such that 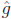(x) = sin(x) =
10.
4. How about f? Yes: Let y ∈ R. Solving y = x3 +1 for x, we obtain x
=
.
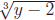Thus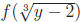 
= y and so f is onto.
5. How about h? No: Let y = 4.5. There is not an x ∈ R such that h(x) = 4.5.
Definition: We can define function composition: Let f : X → Y, g :
Y → Z.
Then g o f : X → Z by g o f(x) = g(f(x)).
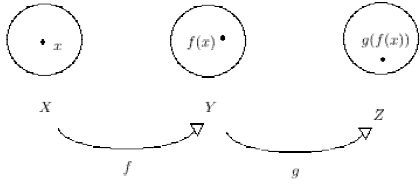
Example: Let f : R → R, g : R → R given by f(x) =
3x + 1, g(x) = 2x2 + x. Then
g o f(x) = g(3x + 1) = 2(3x + 1)2 + (3x + 1).
Theorem: Let f : X → Y and g : Y → Z be functions. If both f and g are
one-to-one, then g o f : X → Z is one-to-one.
Proof: Suppose that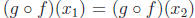 
, where
∈ X. Then
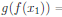
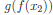. Since g is one-to-one,
. Similarly, since f
is one-to-one,
. Therefore g o f is
one-to-one.
Definition: We sometimes restrict the domain of a function. Let f : X → Y
and let
A 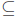X. The restriction of f to A is the
function fA : A → Y given by fA(x) = f(x)
for x ∈ A. In other words, fA = f for all elements of A and is
undefined for all
elements outside of A.
| Prev | Next |