Rectangular Coordinate System , Graphs of Equations and Lines

Section 3.1: Rectangular Coordinate System

· Note 1: The rectangular coordinate system is divide into 4 quadrants : I, II, III and IV.

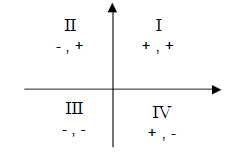
· Note 2: Distance between two points A(x₁,y₁) and B(x₂,y₂) is: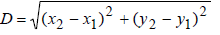

Example 1: Find the distance between A(1, 2) and B(-1, 4)

· Note 3: Midpoint of a line connecting 2 points A(x₁,y₁) and B(x₂,y₂):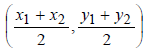

Example 2: Find the midpoint of from A(-1, 4) and B(1, 2)
Example 3: Find a formula that expresses the fact that an arbitrary point P(x, y) is on the perpendicular bisector
l of segment AB: A(-3 , 2) , B(5, -4)

More examples:
Example 4: Find all points on the y-axis that are a distance of 4 from P(3,5)
Example 5: Find all points on the x-axis that are a distance of 5 from P(-2,3)

Section 3.2: Graphs of Equations

1) graph y = -x² + 5

2) graph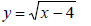

· Symmetric with respect to the y-axis, then f(x) = f(-x) such as: y = x² + 2
· Symmetric with respect to the x-axis, then f(y) = f(-y) such as: x = y² + 3.
· Ssymmetric with respect to the origin, then simultaneous substitution of -x for x and -y for y gets the same
equation such as: 2y = x³

Examples: determine which graphs are symmetric with respect of:
a) the y-axis b) the x-axis c) the origin

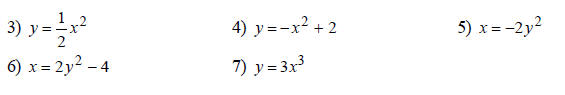
Equation Of The Circle With a Radius r :

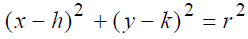
8) Find the equation of the circle with center (-4, 1) and r = 3
9) Find the equation of the circle with center (-2, 4) and passes (2 , 1)
10) Find the equation of the circle with center (4, -1) and tangent to the x-axis.
11) Find the equation of the circle with end points of a diameter A(-5, 2) and B(3,6)
12) Find the center and the radius of x² + y² + 8x - 10y + 37 = 0
13) Find the center and the radius of 9x² + 9y² + 12x - 6y + 4 = 0
14) Find the center and the radius of x² + y² + 4x + 6y + 16 = 0
15) Graph the circle or semicircle: x² + y² = 8
16) Graph the circle or semicircle: (x - 4)² + (y + 2)² = 4
17) Graph the circle or semicircle: x² + y² =16
18) Graph the circle or semicircle: 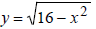(half the circle of example 17 when y is isolated)

19) Graph the circle or semicircle: 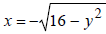(half the circle of example 17 when x is isolated)

Important:

· If 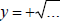, then the graph is the upper half of a circle (see example 18).
· If 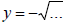, then the graph is the lower half of a circle.
· If 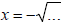, then the graph is the left half of a circle (see example 19)
· If 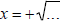, then the graph is the right half of a circle

Book, Exer. 57 - 60: Find the equations for the upper half, lower half, right half, and left half of the
circle:

Book, Exer. 61 - 62: Determine whether the point P is inside, outside, or on the circle with center C
and radius r :

62) (a) P(3,8), C(-2,-4), r = 13
(b) P(-2,5), C(3,7), r = 6
(c) P(-2,5), C(3,7), r = 6

Book, Exer. 63 - 64: For the given circle, find (a) the x- intercepts and (b) the y-intercepts:
64) x² + y² -10x + 4y + 13 = 0

Section 3.3: Lines

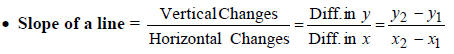
1) Find the slope of the line passing the points (-2, 4) and (3, -1)
2) Find the slope of the line passing the points (2,-3) and (-1, 3)

· m > 0 or positive slope , then the line is increasing or rising
m < 0 or negative slope , then the line is decreasing or falling
m = 0, then the line is horizontal
m = undefined, no slope, then the line is vertical
3) graph the line that passes the point P(2 , 4) and has m = -1/3

· Slope -Intercept Equation:

y = mx + b (m is the slope, b is the y-intercept)

Find the slope and the y-intercept for:

4) 4x + 2y = 5
5) 3y - 2x = 5 + 9y – 2x
6) 5x = 2/3 y - 10
7) y = 10
8) x = 5

· General Linear Equation :

ax + by = c

Note: isolate y in the above equation and you will get:

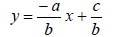
Compare it to the Slope-Intercept Equation: slope = -a/b and the y-intercept = c/b.

Graphing a Linear Equation:
· Using the x and y-intercepts ( x-intercepts when y = 0 ; y-intercepts when x = 0)

9) 4x - 5y = 20
10) 3x + 2y = 12
11) 2y - 3x = 0

· Using Slope -Intercept Equation (isolate y to get y = mx + b)

12) 2y - 3x = 0
13) -2x + y = 3

· Special Cases:

14) y = 3 15) x = 5 16) y = 0

Finding the equation of a line: y = mx + b (or ax + by = c)

· Case 1: One point is given and the slope:
Find the equation of the line having the given slope and containing the given point:
17) m = -2 ; (2, 8) 18) m = -4/5 ; (2, 3)

· Case 2: Two points are given:
Find the equation of the line containing the given pair of points:
19) (2, -1) and (1, -3)

20) (-1, -5) and (2 , 1)

Parallel and perpendicular lines:

· Two lines are parallel if they have same slope but different y -intercepts.
Example: y = 3x – 4 and y= 3x –2 where the slope is = 3 in both

· Two line are perpendicular if the slopes are m and –1/m ( multiplication of both slopes = -1)
Example: y = 2x - 5 and y= -1/2 x + 3 where m = 2 and m = -1/2

Find an equation of the line containing the given point and parallel to the given line:
21) (2, -1) ; 2y + 10 = x 22) (-8, 4) ; 2y - 2x = -17
Find an equation of the line containing the given point and perpendicular to the given line:
23) (-3, 4) ; y - 3x = -2 24) (2, -3) ; 2y + 4x = 1
Find an equation of the perpendicular bisector of the segment AB:
25) A(4, 2) , B(-2, 10)

Applications:
26) The cost of producing 100 units is $60 and for 120 units is $70. Find the equation, and the cost
of 200 units