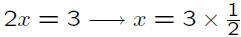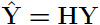Matrix Approach to Simple Linear Regression

Use of Inverse

• Consider equation

• Inverse similar to using reciprocal of a scalar

• Pertains to a set of equations

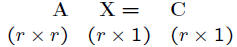
• Assuming A has an inverse:

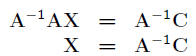
Random Vectors and Matrices

• Contain elements that are random variables

• Can compute expectation and (co)variance

• In regression set up, 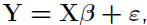both ε and Y are random
vectors

• Expectation vector:

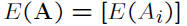
• Covariance matrix: symmetric

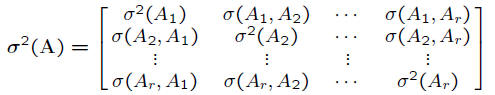
Basic Theorems
• Consider random vector Y

• Consider constant matrix A

• Suppose W = AY
– W is also a random vector
– E(W) = AE(Y)
–

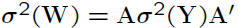
Regression Matrices

• Can express observations
Y = Xβ +ε

• Both Y and ε are random vectors

E(Y)
= Xβ+E(ε)
= Xβ

Least Squares

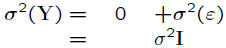
• Express quantity Q

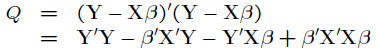
• Taking derivative →

• This means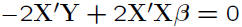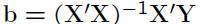

Fitted Values

• The fitted values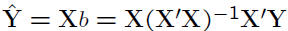

• Matrix 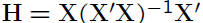is called the hat matrix
– H is symmetric, i.e., H' = H
– H is idempotent, i.e., HH = H

• Equivalently write

• Matrix H used in diagnostics (chapter 9)

Residuals

• Residual matrix

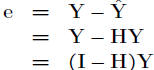
• e a random vector

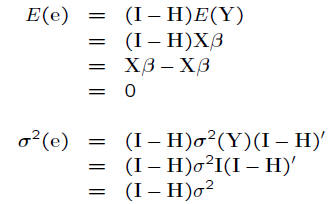
ANOVA

• Quadratic form defined as

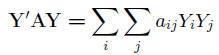
where A is symmetric n × n matrix

• Sums of squares can be shown to be quadratic forms (page
207)

• Quadratic forms play significant role in the theory of linear
models when errors are normally distributed

Inference

• Vector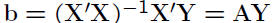

• The mean and variance are

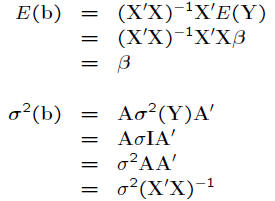
• Thus, b is multivariate Normal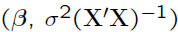

• Consider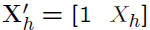

• Mean response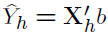

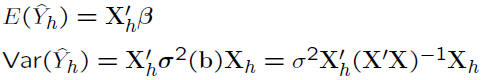
• Prediction of new observation

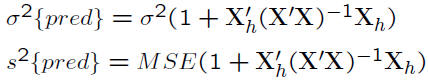
Chapter Review

• Review of Matrices

• Regression Model in Matrix Form

• Calculations Using Matrices