Merit Worksheet #14
1. Find the derivative of each of the following functions:
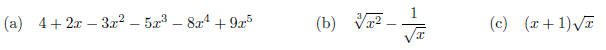
2. Find the equation of the line tangent to y = x^2 at the point (2, 4).
3. Find the derivative of the following functions, once with the Product Rule , and once without it.
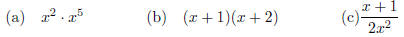
4. State in your own words what the product rule is . Can you come up with a
product rule for three
functions (with an explanation)? In other words, find a formula for
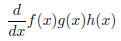
and convince me that your answer is correct.1
5. Review with your group what the Quotient Rule is for derivatives. Then
find the derivative of each of
the following:
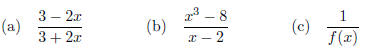
6. Can you use the Quotient Rule to prove the Product Rule? In other words,
can you use the Quotient
Rule to take the derivative of f(x)g(x)?2
7. Find the first, second, and third derivatives of f(x) · g(x). Then
multiply out (a + b)1, (a + b)2, and
(a + b)3. Do you see a pattern? Will that pattern continue for higher
derivatives/powers? Can you
explain why the pattern happens?
8. (a) Now let’s think of things differently . Find
functions whose derivative are 1, x, x2, x3, and x4.
Can you find a formula for a function whose derivative is xn?
(b) Does your answer to part (a) tell you of a function whose derivative is x-1?
9. Using your good old-fashioned limit definition of the
derivative and a calculator, approximate what
the derivative of ln x is at x = 1, x = 2, and x = 3. Can you guess a formula
for the derivative of ln x?
10. And now for a little something to pass the rest of the
time: We have a very easy way to tell if a quadratic
equation has zero, one, or two solutions —we use the quadratic formula, and the
discriminant b2 − 4ac
in particular.
(a) How many solutions does the equation x2 − 6x + 10 = 0 have? How do you know?
Suppose you want to learn about a cubic function f(x) = x3
+ px2 + qx + r. Answer the following
questions.
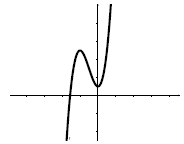
(b) Some cubic functions, like x 3 + 3x2
+ 1, have two “bends” in their graphs, as shown below.
Others, like x3 and x3 + x, are increasing the whole time
and never bend downwards. Using the
formula for f(x) above, and the derivative f′(x), which you can calculate using
the power rule ,
how can you tell if f(x) has two bends, or none?
(c) How many real zeros can a cubic function have if it
never bends downwards? How many can it
have if it has two bends?
(d) How could you use the Intermediate Value Property and
the previous parts to determine how
many real solutions the equation
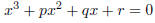
has?
(e) Without graphing anything , tell how many real zeros these polynomials have:
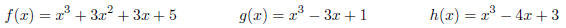
11. Using the Product Rule, find the derivatives of [f(x)]2,
[f(x)]3, and [f(x)]4. Based on your answers to
these and to Problem 5 part (c), complete the formula:
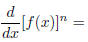
You’ll learn more about derivatives of this type when you learn the Chain Rule in lecture today.
| 1And if you can do that, make a guess
as to what the Product Rule would be for a product of n functions. How
would you go about proving your guess? 2The answer is yes. Now do it. |
| Prev | Next |