Module on Relating and Comparing
Module on Relating and Comparing Fractions and Decimals for Grades
Total Score___________
Grade 5-6 Pretest Form A
Name ____________________________________________ Date_______________
Be sure to follow the directions for each problem.
Solve.
1. Express the shaded areas as both a fraction and a decimal .
a)

Fraction _________
Decimal _________
b)

Fraction ________
Decimal ________
2. Draw a picture that represents 3/5.
3. Draw a picture that represents 0.4.
4. Write a fraction of your choice and its equivalent decimal.
| Fraction | Decimal |
| _______ = _______ | |
5. a) How much money is ¼ of a dollar? Write it with a
decimal point .
_____________
b) Explain how you got your answer.
6. Juan drank a 0.5 liter bottle of Mountain Dew with his lunch. What fraction
of a
liter did he drink?
_______________
7. Order the following from least to greatest: 0.75 , 1/3 , 4/5 , 0.2
___________________________________
8. a) Susan and Tina were the first to finish in a swimming race. Susan swam
the race in 0.3 hour. Tina’s time was 1/5 hour. Who won the
race?
_______________
b) Explain how you arrived at your answer.
Lesson 1: Converting Decimals to Fractions
Objective: Students will be able to convert decimals to fractions in their
lowest form.
Standards Addressed:
Show-Me Goals:
• 1.2 – Students will demonstrate within and integrate across all content areas
the ability to conduct research to answer questions and evaluate information and
ideas.
• 2.3 – Students will demonstrate within and integrate across all content areas
the
ability to exchange information, questions and ideas while recognizing the
perspectives of others.
• 4.6 – Students will demonstrate within and integrate across all content areas
the
ability to identify tasks that require a coordinated effort and work with others
to
complete those tasks.
Missouri Frameworks for Curriculum Development:
• Mathematics #1 – In Mathematics, students in Missouri public schools will
acquire a solid foundation which includes knowledge of addition, subtraction,
multiplication and division ; other number sense, including numeration and
estimation; and the application of these operations and concepts in the
workplace
and other situations.
• Mathematics #5 – In Mathematics, students in Missouri public schools will
acquire a solid foundation which includes knowledge of mathematical systems
(including real numbers , whole numbers, integers, fractions), geometry, and
number theory (including primes, factors, multiples).
Introduction and application to everyday life:
Homework assignment the night before lesson 1:
Ask students to bring at least two items from home that use decimals or
fractions..
Examples: rain gauge, stop watch, newspaper articles, soda bottle, pizza price
list, stock
market reports, recipes, etc.
Have a large bulletin board and table prepared upon which to display items.
Label the
bulletin board with DECIMALS AND FRACTIONS.
Lesson:
Ask students to share the items they brought to class. Have them post each
on the
bulletin board or the table. Talk briefly how often we see decimals and
fractions in our
everyday life.
Let’s study the relation between fractions and decimals.
It’s very easy to change decimals to fractions. Just say the decimal and then
write it as a
fraction that would be read the same way.
Examples:
0.3 = three tenths = 3/10
0.57 = fifty-seven hundredths = 57/100
0.131 = one hundred thirty-one thousandths = 131/1000
Sometimes the fractions will need to be reduced to their lowest terms.
Examples:
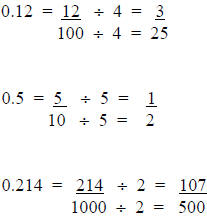
Guided Practice:
Have students form groups of three. In each group one student will write a
decimal on a
piece of paper, the second student will read the decimal, and the third student
will write
the decimal as an equivalent fraction. Students should rotate roles until each
student has
performed each role twice. The students will check each other’s answers.
Independent Practice:
Students complete Worksheet P1
Worksheet P1
Complete the following chart .
| DECIMAL | WRITTEN NAME | FRACTION IN REDUCED FORM |
|
| 1 | 0.12 | ||
| 2 | one tenth | ||
| 3 | 0.607 | ||
| 4 | three hundred seventy-seven thousandths | ||
| 5 | forty- two hundredths | ||
| 6 | 0.9 | ||
| 7 | 0.124 | ||
| 8 | |||
| 9 | 1/2 |
Lesson 2: Converting Fractions to Decimals
Objective: Students will be able to convert fractions to decimals.
Standards Addressed:
Show-Me Goals:
• Goal 1.4 – Students will demonstrate within and integrate across all content
areas
the ability to use technological tools and other resources to locate, select and
organize information.
• Goal 1.5 – Students will demonstrate within and integrate across all content
areas
the ability to comprehend and evaluate written, visual and oral presentations
and
works.
• Goal 1.6 – Students will demonstrate within and integrate across all content
areas
the ability to discover and evaluate patterns and relationships in information,
ideas
and structures.
Missouri Frameworks:
• Mathematics #1 – In Mathematics, students in Missouri public schools will
acquire a solid foundation which includes knowledge of addition, subtraction,
multiplication and division; other number sense, including numeration and
estimation; and the application of these operations and concepts in the
workplace
and other situations.
• Mathematics #5 – In Mathematics, students in Missouri public schools will
acquire a solid foundation which includes knowledge of mathematical systems
(including real numbers, whole numbers, integers, fractions), geometry, and
number theory (including primes, factors, multiples).
Application to everyday life:
The local weatherman recorded 3/4” rain last night. Your science teacher asks
you to
graph the rainfall amount on your class’ rainfall chart. However, in order to do
so, you
must convert that fractional amount to a decimal amount. What decimal amount
equals
3/5” rain?
Lesson:
As you recall from our last lesson, decimals can be converted to fractions. It
only makes
sense that fractions can be converted back to decimals.
Method 1:
Sometimes you can create an equivalent fraction with a denominator of 10 or 100
(the
same name as the first two places on the right side of the decimal point).
Examples:
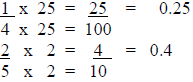
Practice: (Fill in the missing numbers.)
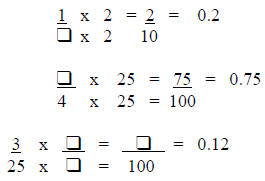
Method 2:
A fraction is nothing more than a division problem. A fraction, read from the
top
downward, is the numerator divided by the denominator.
Example: 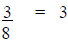 divided by 8 OR
divided by 8 OR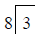
This problem can be solved either :
a) manually by using long division
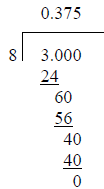
OR
b) by calculator by pressing:
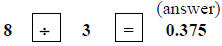
NOTE: If the quotient does not come out even, you may have to round to
the nearest tenth, hundredth, or thousandth, depending on the accuracy level
you are seeking.
Guided Practice: (Practice using all three methods,
when possible.)
4/5 = ___________ 3/4 = ________________
7/10 = ___________ 6/8 = ________________
2/3 = ____________ 4/7 = ________________
6/25 = ____________ 5/12 = ________________
Point of Discussion:
Two different fractions above were equivalent to the same decimal. Why did that
occur?
Write your explanation below
Pair Activity:
Have students form pairs. Give each pair two number cubes that have numbers from
1 to
6. Both students roll their number cube. Have students record the smaller number
as the
numerator and the larger number as the denominator. Both students use
calculators to
find the equivalent decimal.
Students should keep a record of their results on Worksheet P2.
Class Activity:
Show Transparency 1 on the screen. Supply students with calculators. Have all
students
use their calculators to help the teacher fill in the chart. Have students take
turns
vocalizing the answers.
Worksheet P2
| Numerator | Denominator | Fraction | Equivalent Decimal |
Fraction to Decimal Division Table
 |
|||||||
 |
N/D | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | ||||||
| 2 | 3 | ||||||
| 3 | 1.333 | ||||||
| 4 | |||||||
| 5 | |||||||
| 6 | 0.333 |
Lesson 3: Comparing Fractions and Decimals
Objective: Students will be able to compare fractions to decimals and
decimals to
fractions.
Standards Addressed:
Show-Me-Goals:
• Goal 1.5 – Students will demonstrate within and integrate across all content
areas
the ability to comprehend and evaluate written, visual and oral presentations
and
works.
• Goal 1.6 – Students will demonstrate within and integrate across all content
areas
the ability to discover and evaluate patterns and relationships in information,
ideas
and structures.
• Goal 3.4 – Students will demonstrate within and integrate across all content
areas
the ability to evaluate the processes used in recognizing and solving problems.
Missouri Frameworks for Curriculum Development:
• Mathematics #1 – In Mathematics, students in Missouri public schools will
acquire a solid foundation which includes knowledge of addition, subtraction,
multiplication and division; other number sense, including numeration and
estimation; and the application of these operations and concepts in the
workplace
and other situations.
• Mathematics #5 - In Mathematics, students in Missouri public schools will
acquire a solid foundation which includes knowledge of mathematical systems
(including real numbers, whole numbers, integers, fractions), geometry, and
number theory (including primes, factors, multiples).
Application to everyday life:
Tom finished his homework in 3/5 of an hour. Frank completed his homework in .65
of
an hour. Who took longer doing his homework?
Lesson:
• From Korean Mathematics Grade 5-1
Korean Mathematics p. 48

Korean Mathematics p. 49

Korean Mathematics p. 50
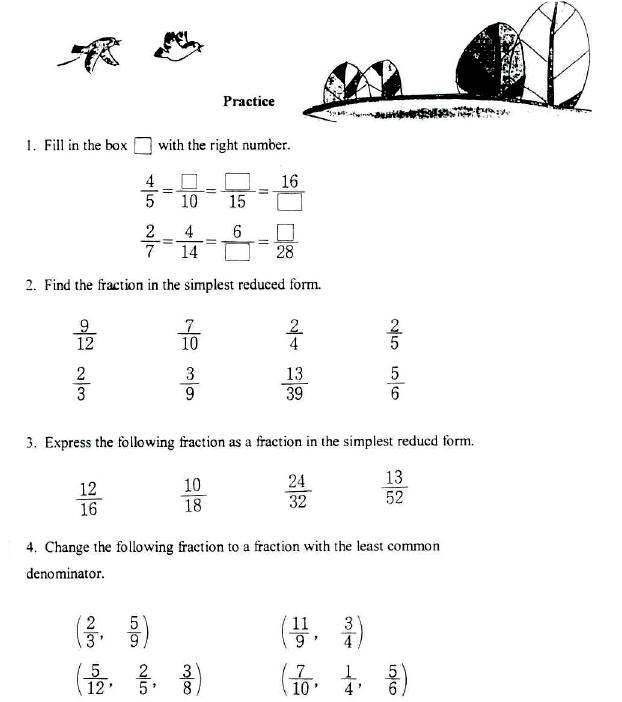
Korean Mathematics p. 51

Total Score _________
Grade 5-6 Posttest Form B
Name __________________________________________ Date _________________
Be sure to follow the directions for each problem.
Solve.
1. Write a decimal of your choice and its equivalent fraction.
Decimal Fraction
________ = __________
2. Draw a picture that represents 0.2
3. Express the shaded areas as both a fraction and a decimal.
a)

Fraction ________ Decimal __________
b)

Fraction ________ Decimal __________
4. Peter ate 3/5 of a pizza last Saturday night. Andy ate
0.7 of a pizza. Who ate the
most pizza?
__________________
Explain how you arrived at your answer.
5. Hans ran the 50 yard dash in 0.9 of a minute. How would you show that amount
as
a fraction of a minute?
__________________
6. a) How much money is 4/5 a dollar? Write it with a decimal point.
_____________________
b) Explain how you got your answer.
7. Draw a picture that represents 7/10.
8. Order the following from greatest to least : 0.3 , 6/7 , 2/3 , 0.45
9. Ralph’s dog, Pogo, is 0.4 ft. tall. Express Pogo’s
height as a fraction of a foot.
__________________________
10.

Rubric
For
Multi-Point Questions
On
Grade 5 – 6 Pretest Form A
#2:
2 pts. – Student draws appropriate picture and indicates the correct number
of parts
1 pt. - Student draws appropriate picture or shades the correct number of
parts
0 pts. - Student indicates no mathematical understanding of the task
#3: (use question #2 rubric)
#5b:
2 pts. - Student demonstrates complete knowledge of mathematical concept
and principles needed to complete the task
1 pt. - Student demonstrates partial knowledge of mathematical concept and
principles needed to complete the task
0 pts. - Student demonstrates no knowledge of mathematical concept and
principles needed to complete the task
#8b:
3 pts. - Response includes all three of the following expectations:
1) clear and understandable explanation of solution processes
2) correctly converts the fraction to a decimal or the decimal to
a fraction
3) correctly compares decimal to decimal or like fraction to like
fraction
2 pts. - Response includes two of the three expectations above
1 pt. - Response includes one of the three expectations above
0 pts. - Response, or lack thereof, indicates no mathematical understanding
of the task
Rubric
For
Multi-Point Questions
on
Grade 5 – 6 Posttest Form B
#2 :
2 pts. – Student draws appropriate picture and indicates the correct
number of parts
1 pt. - Student draws appropriate picture or shades the correct number of
parts
0 pts. - Student indicates no mathematical understanding of the task
#4b:
3 pts. - Response includes all three of the following expectations:
1) clear and understandable explanation of solution processes
2) correctly converts the fraction to a decimal or the decimal to a fraction
3) correctly compares decimal to decimal or like fraction to like fraction
2 pts. - Response includes two of the three expectations above
1 pt. - Response includes one of the three expectations above
0 pts. - Response, or lack thereof, indicates no mathematical understanding of
the task
#6b :
2 pts. - Student demonstrates complete knowledge of mathematical
concept and principles needed to complete the task
1 pt. - Student demonstrates partial knowledge of mathematical concept and
principles needed to complete the task
0 pts. - Student demonstrates no knowledge of mathematical concept
and principles needed
to complete the task
#7 : (use question #2 rubric)
RUBRIC
FOR
PERFORMANCE EVENT
4 pts. - The student’s response fully addresses the performance event.
The response:
• demonstrates knowledge of the mathematical concepts and
principles needed to complete the event
• communicates all process components that lead to an appropriate and
systematic solution
• may have only minor flaws with no effect on the reasonableness of
the solution
3 pts. - The student’s response substantially addresses the performance event.
The response:
• demonstrates knowledge of the mathematical concepts and
principles needed to complete the event
• communicates most process components that lead to an
appropriate systematic solution
• may have only minor flaws with minimal effect on the
reasonableness of the solution
2 pts. - The student’s response partially addresses the performance event.
The response:
• demonstrates a limited knowledge of the mathematical concepts
and principles needed to complete the event
• communicates some process components that lead to an
appropriate and systematic solution
• may have flaws or extraneous information that indicates some lack of
understanding or confusion
1 pt. - The student’s response minimally addresses the performance event.
The response:
• demonstrates a limited knowledge of the mathematical concepts
and principles needed to complete the event
• communicates few or no process components that lead to an
appropriate and systematic solution
• may have flaws or extraneous information that indicates lack of
understanding or confusion
0 pts. - The student’s response is non-existent or indicates no mathematical
understanding of the task.
| Prev | Next |