OTHER TYPES OF EQUATIONS
Objectives:
• Radical Equations
• Equations of Quadratic Form
| Guidelines for Solving Radical Equations |
| • Isolate the radical on one side of the equation. • Raise both sides of the equation the appropriate power to eliminate the radical. • Solve the resulting equation • Check solutions |
Note: It is very important to check your solutions after
solving a radical equation
because raising both sides of an equation to a power sometimes does not produce
an equivalent equation .
Examples:
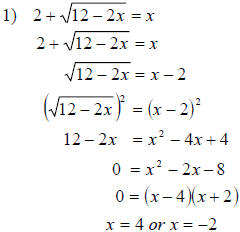
check:
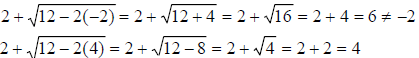
Therefore, the solution set is {4}
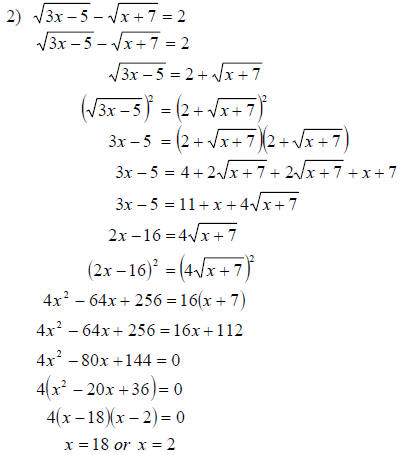
Check:
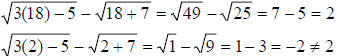
The solution set is {18}
An equation o quadratic form is one that can be written as
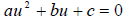 by making
by making
an appropriate substitution .
Examples:
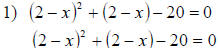
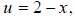 then the equation becomes
then the equation becomes
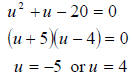
because 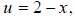 we have
we have
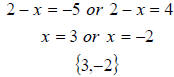
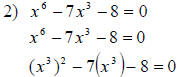
let 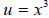 , then the equation
becomes
, then the equation
becomes
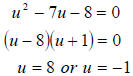
because 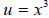 , we have
, we have
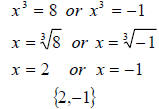
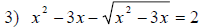
let 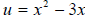 , then the equation becomes
, then the equation becomes
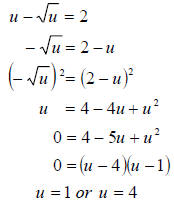
Check: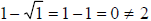
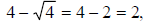 therefore 4 is a
solution , now because
therefore 4 is a
solution , now because 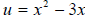 , we have
, we have
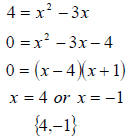
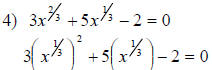
let 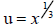 ,then the equation
becomes
,then the equation
becomes
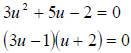
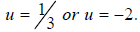 Because
Because
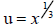 ,we have
,we have
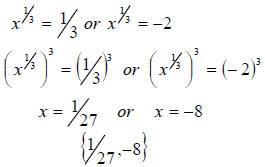
| Prev | Next |