RADIAN MEASURE AND ITS APPLICATIONS

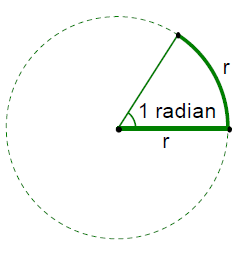
A radian is an angle, which, if its vertex is
placed at the center of a circle , intercepts an
arc equal in length to the radius of the circle.
Note that

2π radians = 1 revolution = 360°and so π radians = 180°.

Thus, 1 radian = 180°/π ≈ 57°.

Very Important: When no unit of measure is indicated on an angle, the
angle is assumed to be expressed in radians.^#

30° means the measure of an angle is 30 degrees;
30 means the measure of an angle is 30 radians.

EXAMPLE 1. Convert 7π/9 to degrees.

EXAMPLE 2. Convert 6.75° to radians.

# Radian measure is a pure measurement (no units). The word "radian" can be dropped from and
inserted into calculations without affecting the value of the expression

EXAMPLE 3. Find the exact value of sin 5π/6

EXAMPLE 4. Find the exact value of cos π.

EXAMPLE 5. Approximate sin 3 to four places after the decimal point.

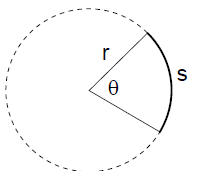
Arc length formula : In a circle of radius r, let an
arc of length s be intercepted by a central
angle θ, measured in radians. Then

s = rθ.

Note: r and s must be measured in the same units.

EXAMPLE 6. The radius of a circle is 100 centimeters. If A and B are two
points on the circle , and if the tangent lines at these points intersect
at point T such that angle ATB is 36°, find the length of minor arc AB.

EXAMPLE 7. Assuming that the earth is a sphere of radius 4000 miles,
find the latitude of Edinburg if Edinburg is located 1800 miles above
the equator. Round to the nearest degree.

Angular and linear velocity : Consider a point P moving with constant
speed on the circumference of a circle with radius r and center O. If
P traverses a distance of s linear units in t time units, then s/t =v is
called the linear velocity of P. If the radius OP swings through θ
angular units in t time units, then θ/t = ω is called the angular
velocity of P. Moreover, if θ is measured in radians and ω is in
radians per time unit, then dividing both sides of s = rθ by t, we get

v = rω.

EXAMPLE 8. The wheels of a bus have a diameter of 80 centimeters and
are rotating at 500 revolutions per minute. How fast is the bus
moving in kilometers per hour? Round to the nearest tenth.

EXAMPLE 9. A belt moving 32 feet per second is driving a pulley at the
rate of 360 revolutions per minute. Find the radius of the pulley in
inches. Round to the nearest tenth of an inch.

HOMEWORK

1. Convert 6π/5 to degrees.

2. Convert 300° to radians

3. Find the exact value of tan 5π/6

4. Find the exact value of cos 3π/2

5. Find the exact value of sin 5π/4

6. In the 1840's there was a border dispute between the United States
and Great Britain over the southern boundary of British Columbia.
The British claimed that the boundary was the 49° latitude, while the
United States said 54.7°. Assuming that the earth is a sphere of
radius 3960 miles, what was the disputed north-south distance?
Round to the nearest mile.

7. An equilateral triangle is inscribed in a circle . Find the length of a
side of the triangle if each side subtends an arc of 28 inches. Round
to the nearest tenth of an inch.

8. The wheels of a car are rotating at 840 revolutions per minute. If the
car is traveling at 55 miles per hour, find the diameter of the wheels in
inches. (1 mile = 5280 feet) Round to the nearest inch.

9. The pendulum of a clock swings through an arc of precisely 8° each
second. If the tip of the pendulum travels 831 centimeters in 1
minute, how long is the pendulum? Round to the nearest tenth.

10. A truck is traveling at 120 kilometers per hour. How many revolutions
per minute are made by the wheels, which are 80 centimeters in
diameter? Round to the nearest integer.

ANSWERS

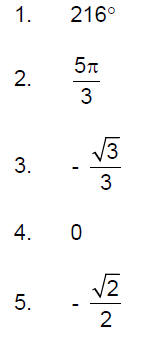
 6. 394 miles
 7. 23.2 inches
 8. 22 inches
 9. 99.2 centimeters
 10. 796 revolutions per minute