Simplifying , Multiplying & Dividing Rational Expressions

To reduce an algebraic fraction : factor first , then cancel
_____________________________.

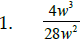
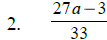
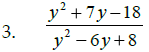
Math 1210 Sec . 5.1 Simp., Mult. & Div. Rational Expr.

To multiply algebraic fractions: factor first, next cancel
__________________________ and then multiply across.

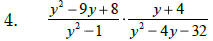
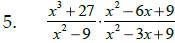
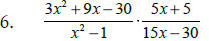
To divide algebraic fractions: factor first, then flip over the
second fraction; ___________________ & multiply across.

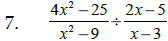
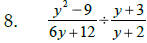
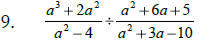
Math 1210 Sec. 5.2 Adding & Subtracting Rational
Expressions

Add or Subtract , as indicated:

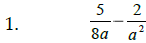Steps: #1: Find the least common denominator #2: Build equivalent fractions #3: Add or subtract numerators (simplify) #4: Reduce, if possible

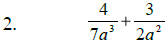
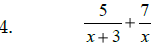
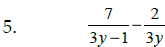
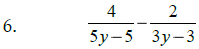Hint: Factor denom. 1st

Expressions

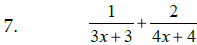
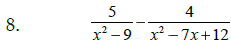
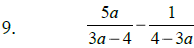
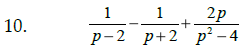
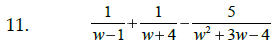
Math 1210 Sec. 5.4 Complex Rational Expressions

Strategy: _____________________________________________
______________________________________________________

Simplify:

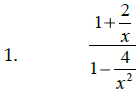
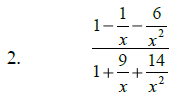
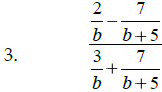
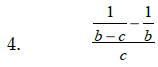
Math 1210 Sec. 5.5 Solving Rational Equations

Strategy: _____________________________________
___________________________________________________

Remember: Always check to be sure that the solution
obtained is actually possible (in the domain).

Solve:

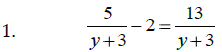
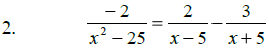
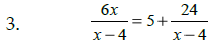
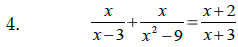
Math 1210 Sec. 5.6 Work and Distance Problems

Work Problems

Use the formula: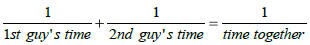

1. Joe can clean the house alone in 5 hours, while Jan
needs only 3 hours. How long will it take them to clean
the house if they work together?

2. Pete can mow and clean up a lawn in 8 hours. If
Sally helps, the job can be done in 6 hours. How long
would it take Sally, working alone, to do the job?

3. A new printer can print checks three times faster than
an old printer. The old printer can print the checks in
30 min. How long would it take to print the checks
when both printers are operating?

4. Tim can put a new roof on a house twice as fast as
Mark. Working together they can roof a house in
4 days. How long would it take Tim to roof the house
if he worked alone?

Distance Problems (if time is the same in both situations)
Use the formula: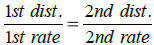

5. The speed of a freight train is 30 mph slower than
the speed of a passenger train. The freight train
travels 140 mi in the same time that it takes the
passenger train to travel 210 mi. Find the speed of
each train.

6. A train travels 100 mi in the same time that a light
plane can fly 260 mi. If the speed of the plane is
80 mph faster than that of the train, find the rate
of each.

7. A boat can travel 100 mi downstream in the same time
that it takes to travel 60 mi upstream. The speed of the
current in the stream is 8 mph. Find the speed of the
boat in still water.

8. An airplane flies 1500 mi with the wind. In the same
amount of time, it can fly 1260 mi against the wind.
The speed of the plane in still air is 230 mph. Find the
speed of the wind.

The formula for this last one is different because the times
are not the same but the total time is given. Use

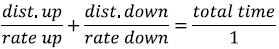
9. A boat moves at 16 mph in still water. It travels 30
miles upstream and then 30 miles downstream in
a total of 4 hours. What is the speed of the current?

Math 1210 Sec. 5.7 Rational Formulas

Use the same strategy as when solving rational equations .

1. Solve 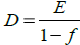for f.
2. Solve 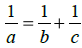for c.

3. Solve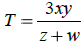 for z.
4. Solve 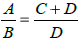for D.
5. Solve 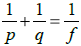for p.

Math 1210 Sec. 5.8 Variation

Direct Variation (when one thing goes up, so does the other)
General format: y = kx

1. The distance an object falls (from rest) varies
directly as the square of the time it falls. If an object
falls 784 ft in 7 sec, how far will it fall in 10 sec?

2. The weight of an object on the moon varies directly
as its weight on earth. A person who weighs 147 lbs
on the earth weighs 24.5 lb on the moon. How much
would a 186-lb person weigh on the moon?

Inverse Variation (When one thing goes up, the other does
down.) General format: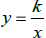

3. The volume of a gas varies inversely as the pressure on
it. The volume of a gas is 160 cm³ under a pressure of
40 kg/cm². What will be its volume under a pressure
of 32 kg/cm²?

4. The time required to empty a tank varies inversely as
the rate of pumping. A pump can empty a tank in
80 min at a rate of 1200 L/min. How long will it take
the pump to empty the tank at a rate of 2000 L/min?

Joint Variation (More than two things involved!)

5. The area of a trapezoid is jointly proportional to its
height and the sum of its two bases. If the area is
60.2 cm² when the height is 8.6 cm and the two bases
measure 4.2 cm and 9.8 cm, find the area when the
height is 6.5 cm, and the two bases measure 3.4 cm and
4.6 cm.

6. The height of a right cylindrical cone is directly
proportional to the its volume and inversely
proportional to the area of its base. If the height is 14
inches when the base is 78.54 sq. in and the volume is
366.52 cu. in., find the height when the base is
153.94 sq. in. and the volume is 1026.25 cu. in.