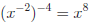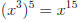Exponents
I. Counting Factors and Laws of Exponents
II. Negative Exponents
III. Rational Exponents
IV. Evaluating Logs
Answers to Exercises
I. Counting Factors and Laws of Exponents
What is the purpose of an exponent? The expression b n indicates that
b (called the base) is a factor n times.
Illustration:
x4 means x is a factor 4 times or x· x· x· x
(x − 2)10 means (x − 2) is a factor 10 times.
To "simplify", express the total number of factors with a single exponent.
| Example | How factor is counted |
 |
x is a factor (4 + 3) times |
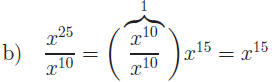 |
x is a factor (25 − 10) times |
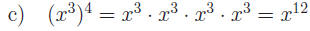 |
x3is a factor 4 times so x is a factor (3 ×4) times |
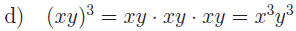 |
xy is a factor 3 times so x AND y are factors 3 times |
Based on these examples, we now state the Laws of Exponents.
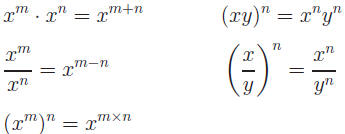
Rather than just memorize, think of these laws |
Exercise 1. Express in simplest form:
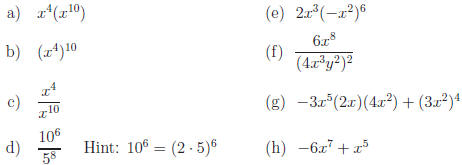
Answers
II. Negative Exponents
If exponents and laws of exponents count factors for positive exponents ,
what does a negative or zero exponent count? This is a hard question to
answer logically so forgive us for just giving definitions.
Def:( )0 = 1 for all ( )
Def: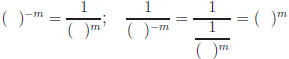
We are using ( ) instead of a variable .
Illustration:
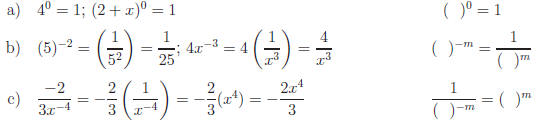
Keep the following in mind when simplifying expressions
with negative ex-
ponents:
1) Exponent laws do not depend on the type of exponent.
2) In a simplified answer all exponents are positive.
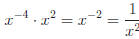
Examples: Express in simplest form.
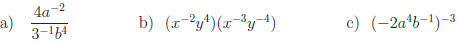
 |
|
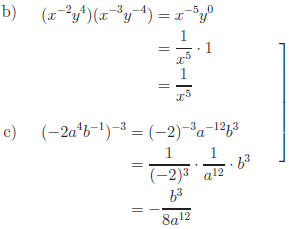 |
Applying exponent laws before manipulating to change negative ex- ponents is the simplest approach. |
Exercise 2. Express in simplest form.
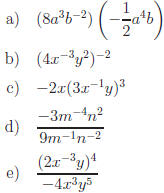
Answers
III. Rational Exponents
Rational ( meaning fractional ) exponents obey the same laws of exponents.
Illustration:
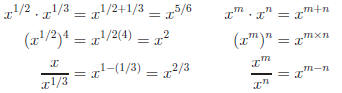
Exercise 3. Simplify.
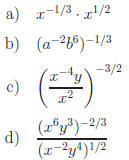
Answer
IV. Evaluating Logs
No study of exponents is complete without some mention of logarithms.
The expression 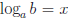 in words is read as "log of b
to the base a = x".
in words is read as "log of b
to the base a = x".
What does this mean?
Answer: 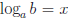 means ax = b.
means ax = b.
Using blanks, 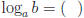 is equivalent to
is equivalent to
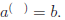
Illustration:
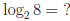 means
means 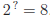 Thus
Thus
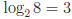 since
since
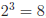 .
.
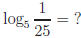 means
means 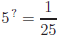 .
Thus
.
Thus 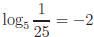 since
since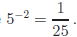
Exercise 4. Evaluate the following.
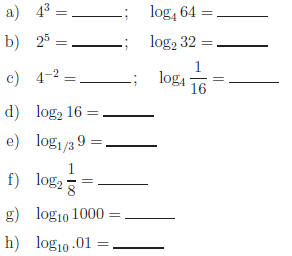
Answers
Beginning of Topic 108 Skills Assessment
Express in simplest form:
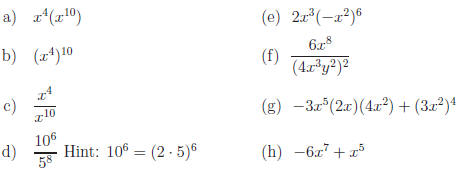
Answers:
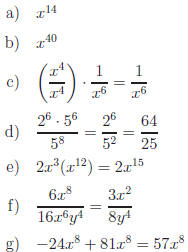
h) Already in simplest form. Sorry for trying to trick
you.
Return to Review Topic
Express in simplest form.
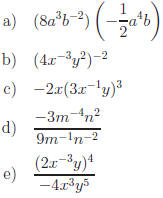
Answers:
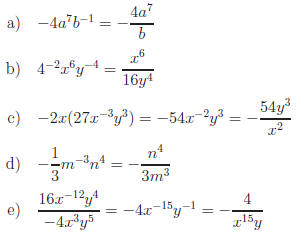
Return to Review Topic
Simplify.
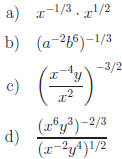
Answers:
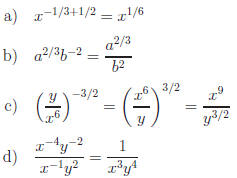
Return to Review Topic
Evaluate the following.
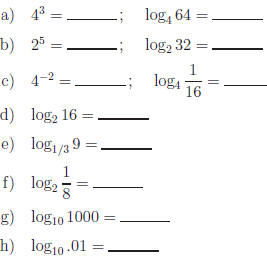
Answers:
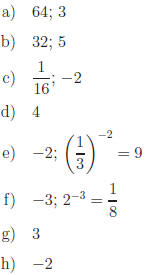
NOTE: Base 10 logs are called common logs and have their
own special
notation. 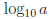 is written as log a. Thus log 1000 = 3 and log
.01 = −2.
is written as log a. Thus log 1000 = 3 and log
.01 = −2.
Return to Review Topic
| Prev | Next |