Single-Variable Calculus

Review of Exponents

Calculus is possibly the greatest single breakthrough in the history of
mathematics. It has applications in nearly every field of science and engineering
and greatly enhances our understanding of the world around us.
What’s really great is that even though calculus is such a powerful tool , it’s
not very hard to learn. There are just two main concepts in calculus; the
derivative and the integral. Both of these deal with rates of change of a
function .

Before diving into calculus itself, it is traditional to review the basic
properties of exponents , logarithms, and functions since these concepts are
so important in calculus. In this first lesson we will focus on exponents.

In mathematics the exponent is simply a short-hand notation for multiplying
a number by itself a certain number of times. For example, if I wanted
to multiply 2 by itself 7 times instead of writing 2 × 2 × 2 × 2 × 2 × 2 × 2 I
could use exponential notation and simply write 2⁷. Or for the more general
case:

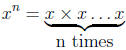
This is the meaning of exponential notation for n as a positive integer,
however exponential notation is also meaningful when n is not an integer
and not positive. The following formulas define the meaning of exponential
notation for these other cases.

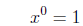	exponent of zero
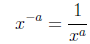	negative exponents
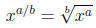	fractional exponents

While these definitions may not seem intuitively obvious, they begin to
make more sense in light of the laws of exponents . These are the four main
laws of exponents.

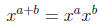	exponent addition
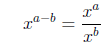	exponent subtraction
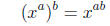	a power raised to another power
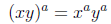	a product raised to a power

These four laws stem directly from the meaning of the exponent for positive
integer powers. They can be derived with some simple algebra , and I
will leave this as an exercise for the reader. Once you are convinced that
these laws are correct, they can then be used to derive the formulas given
earlier for exponents of zero, negative numbers, and non-integers

To illustrate that anything raised to the zeroth power is equal to one, we
can simply divide a number to a power by the same number to the same
power. From elementary school we know that anything divided by itself is
just one, and from the law of exponent subtraction we know that this is also
equal to that number to the zeroth power.

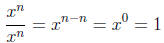
To show that anything raised to a negative power is equal to the reciprocal
of that number raised to the same positive power we can do a similar exercise.
We start by simplifying the following expression using the subtraction law of
exponents.

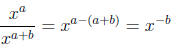
We also could have applied the addition law of exponents to the denominator
of the previous expression .

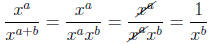
And therefore:

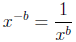
The only thing left to demonstrate is the relation between fractional exponents
and roots. This can also be explained using the laws of exponents.
First of all, let’s see how raising something to the one-half power gives the
square root using our law for raising a power to another power.

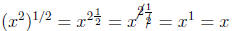
Since x is the square root of x² we can see that raising a number to the
one-half power gives the same answer as if we took the square root. In the
formula above we could just as easily have replaced all the 2’s with some
variable , say a, to obtain a general formula.

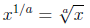
So that we’re not restricted only to numerators of 1, we can apply the
rule for powers raised to a power once again to obtain our final formula.

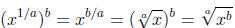
All of these properties of exponents will come in very handy when we
need to simplify expressions into a more calculus-friendly form, or for just
simplifying a final answer to avoid undue embarrassment.

With a little practice the properties of exponents will become second
nature to you if they are not already. If you need practice be sure to try the
problems given in the quiz that accompanies this lesson.