Solving equations in algebra and in arithmetic
Analytic geometry
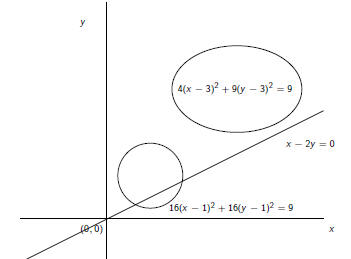
Euclidean geometry
By using Cartesian coordinates , the problems of Euclidean
geometry are translated into algebra problems , many of which can
be further translated into elementary sentences, hence:
Corollary (Tarski, 1930)
Elementary Euclidean geometry is decidable,
—i.e., there is an algorithm which decides whether an arbitrary
(elementary) proposition of Euclidean geometry is true or false
The circle of
Apollonius
The 3-point line and
the 9-point circle of Euler
. . .
There are also very
substantial applications to computer
graphics
Geometry: intuitively simple sentences are not always
elementary
Elementary:
Every angle can be trisected
Not elementary: Every angle can be trisected using ruler and compass
Elementary:
Every cube can be doubled
Not elementary: Every cube can be doubled using ruler and compass
Not elementary: The circle of radius 1 can be squared
(Because π is not an algebraic number)
The elementary (first-order) sentences of geometry are (by
definition) those which can be expressed in the first- order language
of algebra by the use of coordinates
The elementary (first-order) sentences of arithmetic
are exactly the same as for algebra. i.e., the syntactically correct
words (finite sequences) from the alphabet of 16 symbols
| 0 1 + − · = < | ( field operations ) |
¬ (not) & (and) 
(or) |
(sentential operators) |
 (there
exists)  (for
every) |
(quantifiers) |
| ( ) | (punctuation) |
| x | | ( variables x | x|| x||| . . .) |
| - For every number, there is a bigger one | (English) |
 |
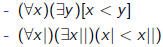(“math-English”) |
| (formal elementary sentence) |
Algebra and arithmetic
“2x + 3 = 0 has a solution”
True in algebra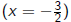 
False in arithmetic
“x4 + 2x3
+ x2 + 5x + 6 = 0 has a solution”
2 solutions in algebra (by Sturm, or more simply)
The integer solutions must divide 6, so we try
0,±1,±2,±3,±6
and verify that the only integer solution is x = −2
Arithmetic is more difficult than algebra!
Theorem (Andrew Wiles, 1994)
The equation xn + yn = zn has no integer
solutions when n > 2
This was conjectured in 1640 by Fermat, who believed he had
proved it, (only the proof “did not fit” in the margin of his
notebook!) and so it is known as Fermat’s Last Theorem, but no
correct proof was known before Wiles’ in 1994
Prime numbers
A number x > 1 is prime if it is divisible only by 1 and x
Primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, . . .
There are 1229 prime
numbers < 10000
There are infinitely
many prime numbers (Euclid)
A number x > 1 is a twin prime if both x and x + 2 are primes
Twin primes: 3, 5, 11, 17, 29, 41, 59, 71, 101, 107, . . .
There are 205 twin
primes < 10000
Are there infinitely
many twin primes?
Open problem (famously and apparently hopelessly for now)
Arithmetical truths
Theorem (Turing, Church, 1936)
There is no algorithm which decides for an arbitrary sentence of
arithmetic whether it is true or false, in other words,
The problem of arithmetical truth is undecidable
Theorem (Matiyasevich 1970,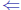 
Davis, Putnam,
Robinson)
There is no algorithm which decides for an arbitrary polynomial
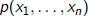with integer coefficients whether the
equation
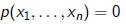
has integer roots , in other words,
Hilbert’s 10th problem is unsolvable
Hilbert 1900: 23 problems
“which will occupy the mathematicians of the 20th century”
How can we prove that a problem is absolutely
unsolvable?
Church-Turing Thesis (1936)
If a function f (α ) on the words from a finite alphabet ∑ can be
computed by some algorithm, then it can be computed by a
program in a computer with an infinitely large hard disk
- The required program can be expressed in any of the usual
programming language (Lisp, Pascal, C, Java, . . . )
- “Infinitely large” means “unbounded”: the computation of
any specific value f (α ) will of course be finite
- Rigorous proofs of undecidability are given by a mathematical
and logical analysis of the computations which can be done by any
computer
- The basic methods for this sort of analysis are due to Kurt
CT: “The first natural law of mathematics ”
| Prev | Next |