The Division Algorithm
Theorem [ Division Algorithm ]. Given any strictly
positive integer d and any integer a, there
exist unique integers q and r such that
a = qd + r,
and
0≤ r < d.
Before discussing the proof, I want to make some general remarks about what this
theorem really
says, why it says it in what seems at first such a perversely obscure way, and
why it's worth proving
something at all which, as we shall see, actually seems quite obvious.
The Language in Which Mathematics Is Done
Even when talking about day to day life, it sometimes happens that one has a
hard time finding
the words to express one's thoughts. Furthermore, even when one believes that
one has been totally
clear, it sometimes happens that there is a vagueness in one's words that
results in the listener
understanding something completely different from what the speaker intended.
Even the simplest mathematical reasoning is usually more complicated than the
most complicated
things one attempts to discuss in everyday life. For this reason, mathematics
has developed an
extremely specialized (and often stylized) language. To see the value of this ,
one only has to think of
how difficult it would be to solve even the simple quadratic equation x 2 − 5x = 14
if one's calculation
had to be done without symbols, using only ordinary language.
"Suppose that a quantity has the property that when five times that quantity is
subtracted from the product of the quantity times itself then the result is 14.
Determine the possible values of this quantity."
During the middle ages, algebraic calculations were in fact done in this fashion
| except that the
language was Latin, not English. But progress beyond the level of simple algebra
only became possible
with the introduction of modern algebraic notation | which the West learned from
the Arabs.
By combining symbolic notation with very precisely defined concepts and a very
formalized
language, any mathematical proof can be expressed in a way that can be
understood by any
"mathematically mature" reader. One is not dependent on the reader's ability to
"see what is meant."
In principle, at least, every step is described in terms so precise that no
possible misunderstanding can
occur, and anyone can follow the reasoning from one step to the next, provided
only that he is skilled
in making the most basic sort of algebraic, set theoretic, and logical
manipulations. In particular, the
language is so explicit that one never needs reference to illustrative examples
in order to explain the
meaning of what is said. (In practice, it has to be admitted that sometimes even
the experienced
mathematician gets stopped at certain points in the proof
and has to rack his brains for a minute or
two |or even longer| before he says, "Oh, yeah, that's why." Students, of
course, have this
difficulty much more frequently.)
It's important to realize, however, that useful as the language of mathematics
is, it doesn't
represent the way humans normally gain understanding. So even something quite
familiar can
sometimes seem strange when described in a precise , mathematical way.
One might think of the language in which mathematics is done as analogous to
programming
languages. A computer program describes how to perform a given task without
omitting even a single
step, no matter how small, and without any conceivable ambiguity. One might
think that for this
reason, a computer program would be the ideal way to explain a procedure so that
no one could
possibly fail to understand it. But in fact, human beings find computer programs
extremely difficult
to understand.
The language of mathematical proofs is a little more human than that of computer
programs.
Nonetheless, learning to read this kind of language is a formidible challenge
for students. Learning to
write it is even more formidible. The endeavor can be quite worthwhile, however,
since the reward for
success is access to the vast realm of modern mathematics.
With this in mind, take another look at the theorem we started with.
Theorem [Division Algorithm]. Given any strictly positive integer d and any
integer a, there
exist unique integers q and r such that
a = qd + r,
and
0 ≤r < d.
One might be excused for racking one's brains for quite some time to figure out
what this theorem
"really means." And yet it simply describes the process of dividing one integer
a (the "dividend") by
another d (the 'divisor") to get a quotient (q ) and a remainder (r ). For
instance,
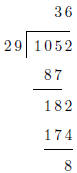
In this example, we have a = 1052 and b = 29. The theorem
above states that there exist unique
numbers q and r such that
1052 = 29q + r and 0 ≤r < 29.
The calculation shows that in fact, q = 36 and r = 8.
The dividend a for the Division Algorithm is allowed to be negative . In this
case, the quotient will
also be negative (or possibly 0), but the remainder is still required to be
positive.
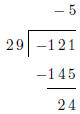
This calculuation represents the equation −121 = 29(−5) +
24.
Operational, Procedural, and Notational Definitions
The statement of the division algorithm as given in the theorem describes very
explicitly and
formally what long division is. To borrow a word from physics, the description
of long division by the
two conditions a = qd + r and 0 ≤r < d is operational. Given two numbers, for
instance, 1052
and 29, the conditions give a very explicit way of testing whether or not 36 is
the quotient and 8 the
remainder when the first number is divided by the second.
On the other hand, these two conditions are not procedural: they do not provide
a recipe for
actually finding the quotient and remainder. In fact, until one recognizes what
the theorem is
describing as simply long division, it is not obvious that the theorem is even
true. Good definitions in
mathematics must always be operational (at least in some idealized sense), but
they are often not
procedural.
Analogously, consider the definition of the absolute value function give in many
college algebra
courses:
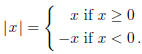
This definition is both operational and procedural, since
it describes exactly how to compute lxl .
And yet most students find it completely bewildering. (Students who do make some
attempt to make
sense out of it often think it says, "If x is positive, leave it alone, and if
it's negative, make it
negative." They forget that if x is negative, then −x if positive: for instance,
−(−13) = 13. )
Unless I consider a student fairly bright, when he asks me what the above definition of the
absolute value function really means, I usually say, "Just make x positive by
throwing away the minus
sign if it has one." One can say that this second definition ("throw away the
minus sign") is
operational and procedural, since it certainly enables one to easily compute the
absolute value of a
number. So what's the advantage of the first one, which seems so bewildering?
Well, for one thing, the first definition of the absolute value function is stated
in terms of intrinsic
properties of numbers, whereas the second definition is notational: it is stated
in terms of the way
we write numbers down. The second definition works fine when we want to computer
the absolute
value of a concrete number written down specifically, but it's not so useful when
we want to talk
about numbers in generality, or we have a number that's not described in
concrete form. (For
instance, if we say "Let x be the smallest solution of the
equation x2 − x = 5," there's no minus sign
in the way we've named x, even though one can show that it is negative.) Most
important, the first
definition is useful for proving theorems, whereas the second is not.
Nonetheless, I think that giving the first definition in college algebra books is
approaching
mathematics in an overly formalistic way that drives many students away.
By the time a student gets to Number Theory, however, it's time he should begin
to learn the kind
of language that is used in contemporary mathematics.
In general, there are often two approaches to defining a mathematical entity. The
procedural
approach gives a method for actually calculating or constructing that entity.
Alternatively, an entity
can be defined by specifying a set of rules which characterize its "behavior" (as
it were). The
mathematics of the Twentieth Century tends to put emphasis on the rules by which
entities behave, rather on the way they are constructed.
As an example of this modern approach, one might describe the natural logarithm
as a function L
with the properties that L(xy) = L(x) +L(y) for all x and y, and L'(1) = 1. This definition says
nothing about how to actually compute the natural logarithm. In fact, until one
has proved the
appropriate theorem, it is not even clear that this natural logarithm function
even exists. However
once the necessary existence theorem has been proved, this modern definition
enables one to derive all
the important formulas for the logarithm function (including the formulas for
its derivative and
integral) in a very clean manner.
The description of long division given in elementary school is notational. From
a mathematician's
point of view, it doesn't describe what long division really is in an intrinsic
way, as the theorem does.
Furthermore, the elementary school definition would not make any sense to someone
who used Roman
numerals or some other non-standard way of writing numbers. (Although the use of
Roman or
Chinese systems for representing numbers is not of great practical concern,
there is non-decimal
representation of numbers which is of quite great importance| namely the
representation of numbers
in computers. If one were required to write a computer program to do long
division, one would not
want to start from the sixth-grade procedure, although that procedure-suitably
modified-might
provide some useful insight.)
The description of the division algorithm by the conditions a = qd + r and 0 ≤r <
d is complete
without reference to any illustrative example. It's also important to realize,
though, that for us human
beings, simple examples, such as the example of long division given above, are
an important aid in
understanding mathematics. As soon as one gives a simple numerical example for
the Division
Algorithm, the student or the mathematician will almost instantly say, "Aha!"
The example appeals
to a different sort of understanding, which is more natural for human beings.
Unfortunately, in many
advanced mathematical texts the reader has to construct such examples for
himself. (One can be sure,
however, that the author has constructed such examples. It's just that it's
considered a little
amateurish | perhaps insulting to the reader's intelligence | to include them in
an advanced text.)
The Importance of the Division Algorthm
The Division Algorithm talks about the form of division one first learns about in
elementary
school, where one gets both a quotient and a remainder. Later on, after one
learns about fractions , it
may seem like a rather simple-minded way of thinking about division. I know it
seemed like that to
me. In particular, I was always annoyed by getting that damned remainder term.
Somehow having a
remainder made the division process imperfect, and that was inconsistent with my
idea of
mathematics as a subject where things are always exact.
In Number Theory, however, this is the way of looking at division which is most
useful. And in
fact that apparently annoying remainder turns out to be often much more
important than the
quotient. In computer science, and certain parts of mathematics, ones writes
a mod d
to denote the remainder when a is divided by d. For instance, 1052 mod 29 = 8.
Most books on
number theory do not use this notation, but instead write 1052 ≡8 (mod 29).
As a simple example of why this concept might be useful, consider the question,
"If June 21, 1997
is a Saturday, then what day of the week will July 4 come on in the year 2000?"
To answer this, first
calculate, taking into account that the year 2000 will be a leap year, that
there are
13 + 3 *365 + 1 = 1109 days between June 21, 1997 and July 4, 2001. Then divide
1109 by 7 and see
that the remainder is 3, so that 1109 mod 7 = 3. This tells us that there are a
certain number of full
weeks (158, in fact, since 158 is the quotient when 1109 is divided by 7) plus 3
more days from
June 21, 1997 until July 4, 2001. The full weeks don't matter, so July 4, 2000
will be three days later
than Saturday, namely Tuesday.
This example may seem of rather limited value, but similar situations arise in
mathematical
applications quite frequently, since many mathematical entities are cyclical in
the same way as the
days of the week are. For instance, if one were to ask what the 500th digit in
the decimal expansion of
1/13 is, is would be foolish to compute all 500 digits. Since the decimal
expansion of 1/13,
viz .076923076923..., has a cyclic pattern of length 6, one only need note that
500 mod 6 = 2, so that
the 500th digit in this expansion will be the same as the second digit, namely
7.
| Prev | Next |