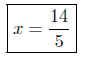Solving Equations & Inequalities
Solutions to Exercises
7.1. Answers:
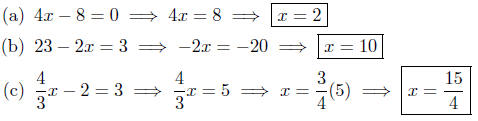
Part (d) on the next page.
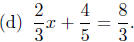
Solution: The most difficult thing about this one is the arithmetic !
 |
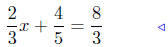given |
 |
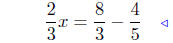subtract 4/5 both sides |
 |
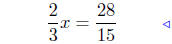arithmetic |
 |
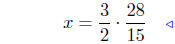multiply both sides by 3/2 |
 |
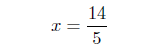7.2. Solutions:
(a) Solve for x :
 |
|
 |
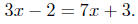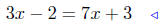given |
 |
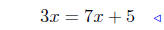add 2 to both sides |
 |
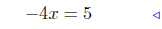add −7x to both sides |
 |
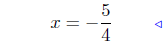divide by −4 |
Presentation of Answer: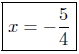
(b) Solve for x:
 |
|
 |
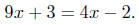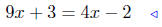given |
 |
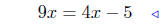add −3 to both sides |
 |
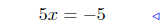add −4x to both sides |
 |
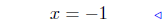divide both sides by −1 |
Presentation of Answer: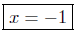
(c) Solve for x:
 |
|
 |
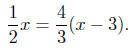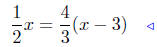given |
 |
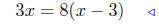multiply both sides by 6 |
 |
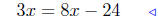expand |
 |
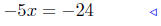add −8x to both sides |
 |
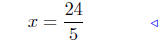divide both sides by 5 |
Presentation of Answer:
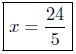
7.3. Answers: Make sure you understand the method of solution .
The answers are given only here.
(a) Solve for x in 5x − 3y = 4.
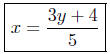
(b) Solve for y in 5x − 3y = 4.
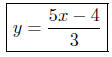
(c) Solve for z in x2z − 12x + y = 1.
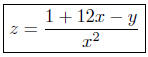
7.4. Solutions:
(a) Solve
 |
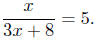
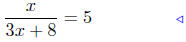given |
 |
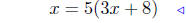mulitply both sides by 3x + 8 |
 |
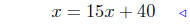expand |
 |
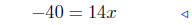add −x − 40 to both sides |
 |
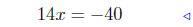transpose |
 |
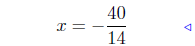divide by 14 |
 |
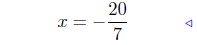reduce fractions |
Presentation of Answer:
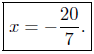
(b) Solve
 |
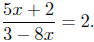
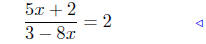given |
 |
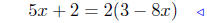multiply both sides by 3 − 8x |
 |
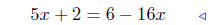expand r.h.s. |
 |
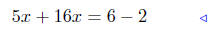add 16x − 2 to both sides |
 |
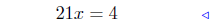combine similar terms |
 |
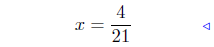divide by 21 |
Presentation of Answer: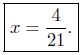
(c) Solve (2x − 3)2= (2x − 7)2.
 |
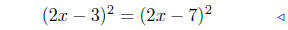given |
 |
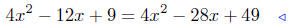expand using (5), Lesson 5 |
 |
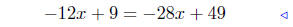add −4x2 to both sides |
 |
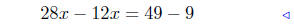add 28x − 9 to both sides |
 |
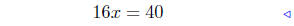combine |
 |
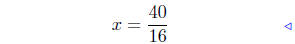divide by 16 |
 |
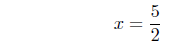Presentation of Answer: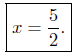
Comment: This problem is similar to (a) of Example 7.2; however, in
my solution I gave a more “traditional’ solution. In the second line
above, I simply expanded the binomials —this is perhaps what you
did yourself. The rest follows using standard methods.
(d) Solve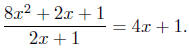 
 |
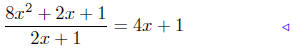given |
 |
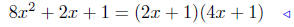multiply both sides by 2x+1 |
 |
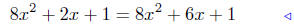expand using (2) of Lesson 5 |
 |
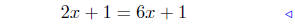add −8x2 to both sides |
 |
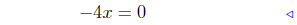add −6x − 1 to both sides |
 |
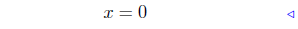divide both sides by −4 |
Presentation of Answer: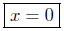 
Now what do you think of that!
7.5. Solutions:
(a) Solve for x: x2 − 7x+12 = 0.
x2 − 7x+12 = 0
(x − 3)(x − 4) = 0
therefore, either
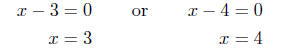
Presentation of Solution:
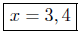
(b) Solve for x: x2 + 3x = 10.
x2 + 3x = 10
x2 + 3x − 10 = 0
(x + 5)(x − 2) = 0
therefore, either
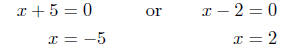
Presentation of Solution: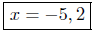
(c) Solve for x: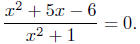 
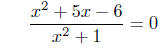
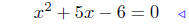mulitply both sides by x2+ 1
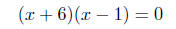
therefore, either
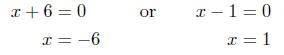
Presentation of Answer: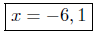 
7.6. Answers:
(a) 12x2 − 17x+6 = 0
 |
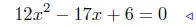given |
 |
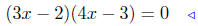factor it ! |
From this we can see that the solutions are
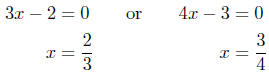
Presentation of Solutions: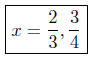 
(b) 20x2 + 3x = 2.
 |
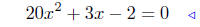add −2 to both sides |
 |
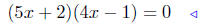factor it! |
Thus,
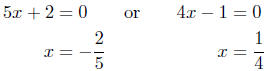
Presentation of Solutions: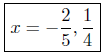 
(c)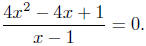 
 |
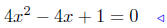multiply both sides by x − 1 |
 |
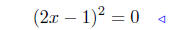factor it– perfect squrare ! |
Presentation of Solution:
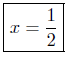
7.7. Answers:
(a) x3 − 2x2 − 3x = 0. Factoring this we obtain
x(x2 − 2x − 3) = 0
x(x − 3)(x + 1) = 0
Presentation of Solutions: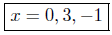 
(b) x4 − 16 = 0. Let’s factor—difference of two squares!
(x2 − 4)(x2 + 4) = 0
(x − 2)(x + 2)(x2 + 4) = 0
Presentation of Solutions: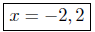 
Comments: The last factor x2+4 is an irreducible quadratic—it
cannot be factored.
(c) x4 − 2x2 − 3 = 0. This is a quadratic equation in the variable
x2: (x2)2 −2(x2)−3 = 0. If you don’t understand what I mean,
temporarily put y = x2; our equation becomes y2 − 2y −3 = 0.
This is clearly a quadratic in y , but y = x2, so it is a quadratic
in x2. Let’s factor it using the factoring techniques.
 |
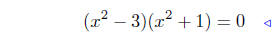factor! |
 |
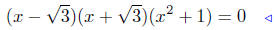again! |
My the Zero -Product Prinicple, we then have
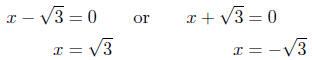
Presentation of Solutions: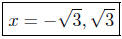 
(d) x4 − 5x2 + 6 = 0. This is again quadratic in x2.
 |
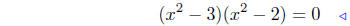factor! |
 |
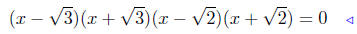again! |
By the Zero-Product Prinicple, we then have
=> 
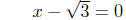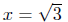
or,
=> 
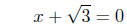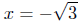
or,
=> 
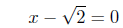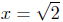
or,
=> 
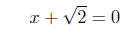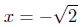
Presentation of Solutions: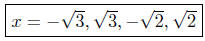 
7.8. Solutions:
(a) Solve for x: 8x2 − 2x − 1 = 0.
 |
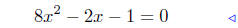given |
 |
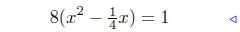Steps 2 & 3 |
 |
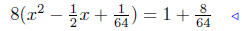Step 4 |
 |
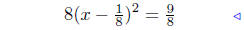perfect square |
 |
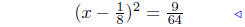divide by 8 |
 |
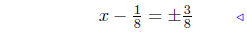take square root |
 |
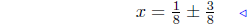add 1/8to both sides |
Presentation of Solutions: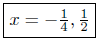 
Comments: Here, mysolution uses a slight variation in the techniques
illustrated in the examples. Rather than having all term
on the left-hand side, I took the constant term to the right -hand
side, then when I completed the square, I added 8/64 to both sides
of the equation.
(b) Solve for x: 3x2 + 5x − 2 = 0.
 |
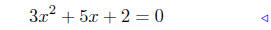given |
 |
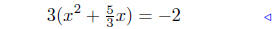Steps 2 & 3 |
 |
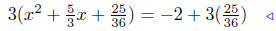Step 4 |
 |
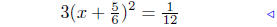perfect square |
 |
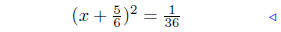divide by 8 |
 |
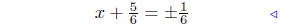take square root |
 |
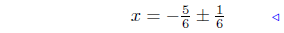add 1/8to both sides |
Presentation of Solution:
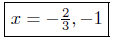
(c) Solve for x: x2 + x − 1 = 0.
 |
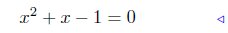given |
 |
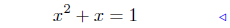Steps 2 & 3 |
 |
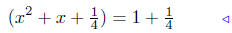Step 4 |
 |
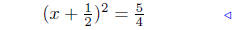perfect square |
 |
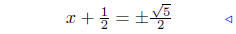take square root |
 |
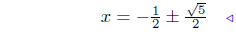add −1/2 to both sides |
Presentation of Solution:
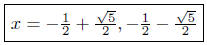or,
Presentation of Solution: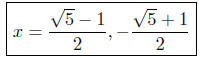
(Verify!)
7.9. Solutions:
(a) Solve for x: 2x2 + 5x − 12 = 0.
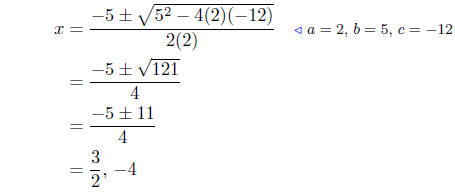
Presentation of Solution: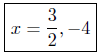
(b) Solve for x: 3x2 − 7x+1 = 0
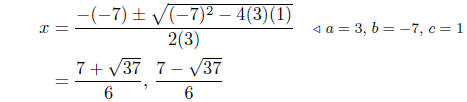
Presentation of Solutions: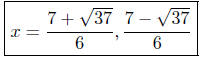 
(c) Solve for x: x2 +1 = 0
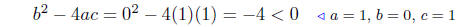
Therefore, this equation has no solutions .
(d) Solve for x: x2+x = 3. Begin byputting it into the proper form:
x2 + x − 3 = 0.
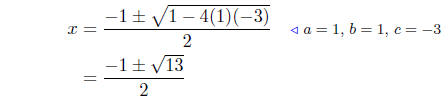
Presentation of Solutions: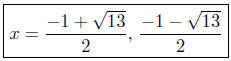 
| Prev | Next |