The Exponential Function

The Story

Speed O’Fender, a TAMS student, just received his driver’s license. He talked his father
into letting him drive a car back to TAMS after a closed weekend. He noticed that just as
he passed the 60 mile marker, the speedometer read exactly 60 miles per hour. A mile later
he passed the 61 mile marker and he happened to be traveling at 61 miles per hour. Speed
decided that it would be fun to always travel at the speed corresponding to the mile marker.
For example, when he was at the 61.5 mile point, his speed was 61.5 miles per hour. When
he reached the 72 mile marker, he was traveling exactly 72 miles per hour. When he was at
the 80 mile marker, he was introduced to a member of the Texas State Police who did not
have enough mathematical or scientific curiosity to encourage Speed in this experiment.

This experience suggested several interesting problems to Speed. First, is the function
s(t) that describes Speed’s position at time t an exponential function ? Second, could this
idea be used to define the exponential function instead of defining it as the inverse of the
logarithm function ? Third, if we define the exponential function using this idea, could we
derive the usual properties of the exponential function? Fourth, is a minimization problem:
How should Speed tell his parents that he got a ticket for speeding in order to minimize the
negative consequences ?

Speed went to you for help with these problems. Your job is to follow the outline below
to help Speed understand how to define the exponential function using a simple differential
equation.

Background Information

It will be helpful to use a theorem from differential equations that we will not cover in class.
The theorem is a special case of an existence and uniqueness theorem that you will learn
when you take a differential equations class.

Example The function f(x) satisfies

f'(x) = f(x) for all x,
f(10) = 0.

Show that f(x) = 0 for every real number x.

Solution Since f'(x) = f(x), f(x) satisfies the differential equation y' = y. So f(x) satisfies
the inital value problem:

y'= y
y(10) = 0.

Let g(x) = 0 for every x. Then g'(x) = 0 = g(x) for every x. We see that g(x) satisfies
the same initial value problem:

y' = y
y(10) = 0.

The uniqueness part of Theorem 1 says that there is only one solution to this inital value
problem. Therefore, f(x) = g(x) = 0 for every real number x.

Some initial value problems have more than one solution, while others have no solution.
An example is the differential equation x³y' = y. With the initial condition y(0) = 1 there
is no solution, but with the initial condition y(0)=0 there are infinitely many solutions.

Directions

Follow the outline below to give a reasonable definition of e^x. From high school algebra, we
know how to define e^x for any rational number. The problem is that we cannot define e^x for
irrational numbers using only precalculus mathematics . In the steps below , you will define
the function E(x) and derive some of its basic properties. In the end you will conclude that
it is reasonable to define e^x to be E(x) for all numbers, rational or irrational. Be careful not
to assume anything about the function E(x) other than its definition and what you have
already proved about it.

You do not have to follow the steps below in exactly the order given. The goal is simply
to define E(x) as stated below and then derive the formula in step 10. If you wish to do
things in a different order, that is fine. However, keep in mind that the outline was designed
to allow you to break the bigger problem in smaller parts. For most of the parts, you will
probably wish to use what you proved in a previous part.

1. Explain why Speed’s position is modeled by the differential equation y' = y. We
normally use t as the variable representing time, but for the remainder of the project
let’s use x. So y is a function of x.

2. Let’s define E(x) to be the unique solution to

y'= y,
y(0) = 1.

Explain why E' (x) = E(x). What is E(0)? Find a formula for E''(x).

3. Use the chain rule to determine the derivative 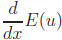, where u is a function of x.

4. Prove that

E(a + x) = E(a)E(x),

where a and x are any numbers. (Hint: Think of a as a fixed number and x as a
variable. Use the uniqueness part of Theorem 1.)

5. Use induction to prove that E(nx) = (E(x))ⁿ for any positive integer n and any real
number x. (Hint: Fix x and then do an induction proof.)

6. Now, let’s define e = E(1). Prove that E(n) = eⁿ for all positive integers n.

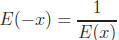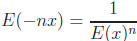7. Prove that for any real number x. Conclude that for
every positive integer n and every real number x. (Hint: This one is not hard!)

8. Prove that E(x) > 0 for all x. Where is E(x) increasing? Where is E(x) concave up?
(Hint: Use the uniqueness part of Theorem 1 to show E(x) ≠ 0 for any value of x. You
may wish to read the example after Theorem 1 again.)

9. Prove that for any positive integer n and any number x, 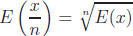. Recall that
for r > 0 and n a positive integer, 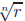is defined to be the unique positive number whose
n^th power is r.

10. Prove that 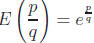for any integers p and q ≠ 0.

11. Explain why it is reasonable to define e^x = E(x) for every real number x.