The Story of a Number

TABLE 1.1 Powers of 2

Of course, such an elaborate scheme is unnecessary for computing strictly with integers; the method would be of
practical use only if it could be used with any numbers, integers, or fractions. But for this to happen we must first fill in
the large gaps between the entries of our table. We can do this in one of two ways : by using fractional exponents, or
by choosing for a base a number small enough so that its powers will grow reasonably slowly. Fractional exponents ,
defined by 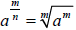( for example, 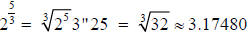) were not yet fully known in Napier's
time, so he had no choice but to follow the second option. But how small a base? Clearly if the base is too small its
powers will grow too slowly, again making the system of little practical use. It seems that a number close to 1, but not
 too close, would be a reasonable compromise. After years of struggling with this problem, Napier decided on
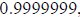or .

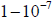But why this particular choice? The answer seems to lie in Napier's concern to minimize the use of decimal fractions .
Fractions in general, of course, had been used for thousands of years before Napier's time, but they were almost
always written as common fractions, that is, as ratios of integers . Decimal fractions - the extension of our decimal
numeration system to numbers less than 1 - had only recently been introduced to Europe, and the public still did not
feel comfortable with them. To minimize their use, Napier did essentially what we do today when dividing a dollar into
one hundred cents or a kilometer into one thousand meters: he divided the unit into a large number of subunits,
regarding each as a new unit. Since his main goal was to reduce the enormous labor involved in trigonometric
calculations, he followed the practice then used in trigonometry of dividing the radius of a unit circle into
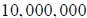or 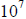parts. Hence, if we subtract from the full unit its 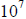th part, we get the number closest to 1 in this
system, namely 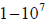and 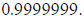This, then, was the common ratio ("proportion" in his words) that Napier
used in constructing his table.

And now he set himself to the task of finding, by tedious repeated subtraction, the successive terms of his progression .
This surely must have been one of the most uninspiring tasks to face a scientist, but Napier carried it through,
spending twenty years of his life (1594-1614) to complete the job. His initial table contained just 101 entries, starting
with 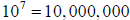and followed by 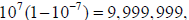then 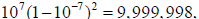and so on up 
to 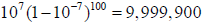(ignoring the fractional pmt .0004950), each term being obtained by subtracting from
the preceding term its 107th part. He then repeated the process allover again, starting once more with , but this
time taking as his proportion the ratio of the last number to the first in the original table, that is,

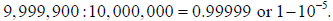This second table contained fifty-one entries, the last being
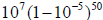or very nearly 9,995,001. A third table with twenty-one entries followed, using the ratio 9,995,001 :
10,000,000; the last entry in this table was 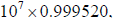or approximately 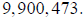Finally, from each entry in
this last table Napier created sixty-eight additional entries , using the ratio 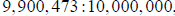or very nearly ;
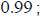the last entry then turned out to be 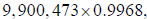or very nearly 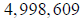- roughly half the original
number.

Today, of course, such a task would be delegated to a computer; even with a hand-held calculator the job could done
in a few hours. But Napier had to do all his calculations with only paper and pen. One can therefore understand his
concern to minimize the use of decimal fractions. In his own words: "In forming this progression [the entries of the
second table], since the proportion between 10,000,000.00000, the first of the Second table, and 9,995,001.222927,
the last of the sums, is troublesome; therefore compute the twenty-one numbers in the easy proportion of 10,000 to
9,995, which is sufficiently near to it; the last of these, if you have not erred, will be 9,900,473.57808."

Having completed this monumental task, it remained for Napier to christen his creation. At first he called the exponent
of each power its "artificial number" but later decided on the term logarithm, the word meaning "ratio number." In
modem notation, this amounts to saying that if (in his first table) 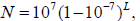then the exponent L is the
(Napierian) logarithm of N . Napier's definition of logarithms differs in several respects from the modem definition
(introduced in 1728 by Leonhard Euler): if where b is a fixed positive number other than 1, then L is the
logarithm (to the base b) of N. Thus in Napier's system  L = 0  corresponds to

 (that is,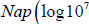),  whereas in the modem system L = 0 corresponds to N=1 (that is ,) Even

 more important, the basic rules of operation with logarithms - for example, that the logarithm of a product equals the
sum of the individual logarithms - do not hold for Napier's definition. And lastly, because is less than 1,
Napier's logarithms decrease with increasing numbers, whereas our common (base 10) logarithms increase. These
differences are relatively minor however, and are merely a result of Napier’s insistence that the unit should be equal to
10 subunits. Had he not been so concerned about decimal fractions, his definition might have been simpler and closer
to the modem one.

In hindsight, of course, this concern was an unnecessary detour. But in making it, Napier unknowingly came within a
hair's breadth of discovering a number that, a century later, would be recognized as the universal base of logarithms
and that would play a role in mathematics second only to the number n. This number, e, is the limit of 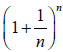as n
 tends to intinity.

NOTES AND SOURCES

1. As quoted in George A. Gibson, "Napier and the Invention of Logarithms," in Handbook of the Napier Tercentenary
Celebration, or Modern Instruments and Methods of Calculation, ed. E. M. Horsburgh (1914; rpt. Los Angeles: Tomash
Publishers, 1982), p. 9.

2. The name has appeared variously as Nepair, Neper, and Naipper; the correct spelling seems to be unknown . See
Gibson, "Napier and the Invention of Logarithms," p. 3.

3. The family genealogy was recorded by one of John's descendants: Mark Napier, Memoirs of
John Napier of Merchiston: His Lineage, Life, and Times (Edinburgh, 1834).

4. P. Hume Brown, "John Napier of Merchiston," in Napier Tercentenary Memorial Volume, ed. Cargill Gilston Knott
(London: Longmans, Green and Company, 1915), p. 42.

5. Ibid., p. 47.

6. Ibid., p. 45.

7. See David Eugene Smith, "The Law of Exponents in the Works of the
Sixteenth Century," in Napier Tercentenary Memorial Volume, p. 81.

8. Negative and fractional exponents had been suggested by some mathematicians as early as the fourteenth century,
but their widespread use in mathematics is due to the English mathematician John Wallis (1616-1703) and even more
so to Newton, who suggested the modem notations a-ll and an/In in 1676. See Florian Cajori, A History of
Mathematical Notations, vol. 1, Elementary Mathematics (1928; rpt. La Salle, Ill.: Open Court, 1951), pp. 354-356.

9. See note 8.

10. By the Flemish scientist Simon Stevin (or Stevinius, 1548-1620). 11. Quoted in David Eugene Smith, A Source
Book in Mathematics (1929; rpt. New York: Dover, 1959), p. 150.

12. Some other aspects of Napier's logarithms are discussed in Appendix 1.

13. Actually Napier came close to discovering the number e, defined as the limit of 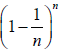as 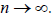As we have
seen, his definition of logarithms is equivalent to the equation 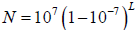If we divide both  N and L by
(which merely amounts to resealing our variables ), the equation becomes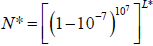and by  where
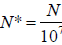
and 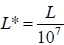. Since 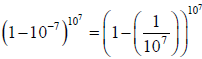 is very close to e, Napier's logarithms are virtually logarithms to
the base e. The often-made statement that Napier discovered this base (or even itself) is erroneous, however. As
we have seen, he did not think in terms of a base, a concept that developed only later with the introduction of
"common" (base 10) logarithms.