A Parent Guide to Mathematics - Grade 5

■ The important math concepts in 5^th grade are extending the operations of addition,
subtraction, multiplication and division of whole numbers to fractions and decimals, and
working with angle measurement. Based on Michigan Grade Level Content Expectations,
the following describes some of the central mathematical skills and understandings that
students should acquire by the end of fifth grade.

■ Number and Operations
Multiply and Divide Whole Numbers

1. Understand how division of whole numbers with and without remainders is
related to multiplication and how division is related to subtraction

2. Multiply a multi- digit number by a two-digit number (e.g., 2787 × 47)

3. Divide up to a four-digit number by any two-digit number

4. Multiply one-digit and two-digit whole numbers by powers of 10
(e.g., 26 × 10 = 260; 26 x 100 = 2600)

Prime Factorizations
5. Find the prime factorization of numbers from 2 through 50 and write the results
using exponents (e.g., 24 = 2 × 2 × 2 × 3 = 2³ x 3¹)

Fractions and Decimals
6. Understand fractions as division statements (e.g., 2 ÷ 3 = 2/3)

7. Express two fractions as fractions with a common denominator (e.g., 1/2 = 3/6
and 2/3 = 4/6 )

8. Understand that decimals and percentages are forms of fractions and be able to go
from one form to any other

9. Write fractions from applied situations in several ways; recognize and find equivalent
ratios (e.g., 3 cups to 5 people, 3:5, an average of 3/5 cup for each person)

10. Add and subtract fractions with unlike denominators of 2 through 12 and with
denominators of 100 (e.g., 3/8 + 7/10 = 30/80 + 56/80 = 86/80)

11. Multiply one-digit and two-digit whole numbers by decimals up to two decimal
places and by powers of 10 (e.g., 35 × 0.1 = 3.5, 8 × 0.25 = 2, 26 × 1000 = 26,000)

12. Multiply two unit fractions with small denominators (e.g., 1/3 × 1/4 = 1/12)

13. Divide a fraction by a whole number and a whole number by a fraction, using simple
unit fractions (e.g., 1/2 ÷ 4 = 1/8 , 4 ÷ 1/2 = 8)

14. Solve applied problems involving fractions and decimals; include rounding
answers and checking reasonableness (e.g., Gamali bought a CD for $9.99 and
the sales tax was 6%. How much did he have to pay for the CD including tax?
Answer: $10.59)

15. Solve for the unknown in equations of the form a + x = b (e.g., 1/4 + x = 7/12)

■ Geometry and Measurement

Area, Volume, and Angles
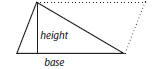
16. Use area formulas and understand and recognize the connections among the
areas of rectangles, triangles, and parallelograms

Example:
area of triangle = 1/2 (base × height)
= 1/2 (area of parallelogram)

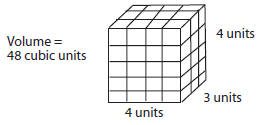
17. Find the volume of cubes and rectangular prisms by filling with unit cubes,
building, counting or measuring

18. Recognize the equivalence of 1 liter, 1,000 ml and 1,000 cm³, make conversions
among liters, milliliters, and cubic centimeters, and know the units of measure
of volume: cubic centimeter, cubic meter, cubic inches, cubic feet, cubic yards,
and use their abbreviations (cm³, m³, in³, ft³, yd ³)

19. Use a protractor or angle ruler to measure angles in degrees; classify angles
as acute (less than 90°), right (equal to 90°), obtuse (greater than 90°), or
straight (equal to 180°)

20. Find the measure of angles formed by intersecting lines, triangles,
and quadrilaterals

■ Data and Probability

Data and Graphs
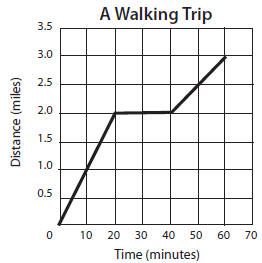
21. Construct and interpret line graphs, and
solve problems based on line graphs
(e.g., the distance-time graph shows a
3-mile trip that lasted 1 hour; the walker
traveled fast for the first 2 miles going
1 mile every 10 minutes, stopped for
20 minutes, then completed the last mile
in 20 minutes, traveling only ½ mile
for every 10 minutes)

22. Find and interpret range, mean, and mode
for a given set of data

Glossary — Grade 5

■ Angle – two rays sharing a common endpoint

■ Exponent – a shortcut notation to express multiplication using the same number
several times (4 is an exponent in 3⁴ = 3 · 3 · 3 · 3 )

■ Factor – positive whole number that divides into a given number with zero
remainder (e.g., factors of 6 are 1, 2, 3 and 6)

■ Line Graph – a visual way to show how two quantities are related to each other and
how one varies according to how the other changes

■ Mean – the sum of the numbers in a list divided by the number of items in the list
(e.g., 4 is the mean of 2, 3, 4, 5, 5, 5 because 2+3+4+5+5+5=24 and 24÷6=4)

■ Mode – the number that occurs most often in a list
(e.g., 5 is the mode of 2, 3, 4, 5, 5, 5)

■ Power of Ten – numbers whose factors can be all tens
(e.g., 1000 = 10 x 10 x 10, so 1000 is the third power of 10)

■ Prime Number – a whole number that has exactly two factors; 1 and the number
itself (e.g., 2, 3, 5, 7, 11)

■ Prime Factorization – writing a whole number as a product of primes
(e.g., 12 = 2 × 2 × 3)

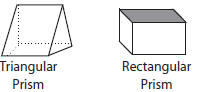
■ Prism – a three-dimensional figure whose bases (ends)
are the same size and shape and are parallel and
whose other sides are parallelograms

■ Quadrilateral – a polygon with four sides

Examples:

■ Unit Fraction – a number written in the form of 1/b, where b ≠ 0 (e.g., 1/2, 1/3, 1/4 . . .)

■ Volume of a Rectangular Three-Dimensional Figure – the number of unit cubes
needed to fill up the inside of the rectangular solid