Quadratic Equations, Inequalities and Functions
Quadratic Equations, Inequalities and Functions
Chapter 11: Quadratic Equations, Inequalities and Functions
• Discuss different methods of solving quadratic equations
• Methods for graphing quadratic equations
• Applications of quadratic equations
Section 11.1: Solving Quadratic Equations using the Square Root Property
• Quadratic equations come in the form of
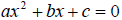 ; standard form
; standard form
• To be able to solve a quadratic equation, it must be in standard form
Zero Factor Property
• If two numbers have a product of zero , then at least one
of the numbers must be zero.
• We use this property to solve equations after they have been factored
Example: Use the zero factor property to solve the given quadratic equation.
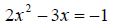
Square Root Property
• If k is a positive number and if
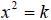 , then
, then
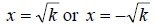
The solution can also be written as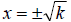
• If the quadratic equation is of the form
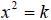 then the square root property can be used
then the square root property can be used
Examples: Solve each equation. Write radicals in simplified form.
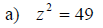
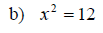
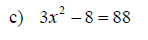
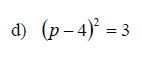
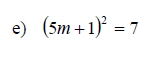
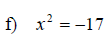
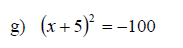
Section 11.2: Solving Quadratic Equations by Completing the Square
• A method for solving quadratic equations
• The goal is to factor the left side of the quadratic equation so that it is a
perfect square
• The right side of the equation is a constant
• The square root property is the used to finish the solving of the equation
• We start with an equation in standard form 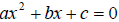
• The end result is of the form 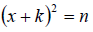
Steps to Complete the Square
1. Make sure a is 1. If a is not 1, then perform the
proper division
2. Write in the form 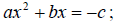 ; variable terms on the
left, constant term on the right
; variable terms on the
left, constant term on the right
3. Complete the square using the formula
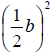
4. Add the value found in step 3 to both sides of the equation
5. Factor the left side as a perfect square, simplify the right side
6. Use the square root property to solve
Examples: Solve the given equations using completing the square.
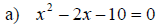
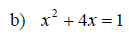
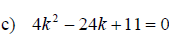
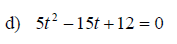
Section 11.3: Solving Quadratic Equations by the Quadratic Formula
• Another method for solving quadratic equations
• Before the quadratic formula can be used the quadratic equation must be in
standard form
Quadratic Formula
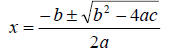
Examples: Use the quadratic formula to solve the given quadratic equations.
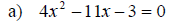
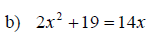
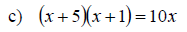
Discriminant
• A part of the quadratic formula;
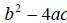
• The discriminant can be used to determine the number and type of solutions a
quadratic equation has
• The following table lays out the types of solutions
| Discriminant | Number and Type of Solutions |
| Positive, and the square of an integer | 2 rational solutions |
| Positive, but not the square of an integer | 2 irrational solutions |
| Zero | 1 rational solution |
| Negative | 2 non-real complex solutions |
Examples: Find each discriminant. Use it to predict the number and type of solutions for each equation.
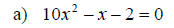
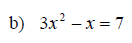
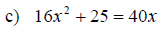
Example: Find k so that the equation will have exactly one rational solution.
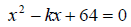
Section 11.4: Equations in Quadratic Form
• We can solve quadratic equations by 4 different methods
-Factoring
-Square Root Property
-Completing the Square
-Quadratic Formula
• Some equations can be simplified down to quadratic form
Example: Solve the given equations
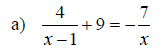
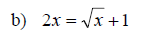
Examples: Solve the given application problems. Use the problem solving steps discussed previously.
1. In 1 ¾ hours Khe rows his boat 5 miles up the river and comes back. The speed of the current is 3 mph. How fast does Khe row?
2. Two chefs are preparing a banquet. One chef could prepare the banquet in 2 hours less time than the other. Together they can complete the job in 5 hours. How long would it take the faster chef working alone?
Section 11.5: Formulas and Further Applications
• This section illustrates the many uses of quadratic equations
• We also look at formulas
Examples: Solve the given formulas for the specified variable.
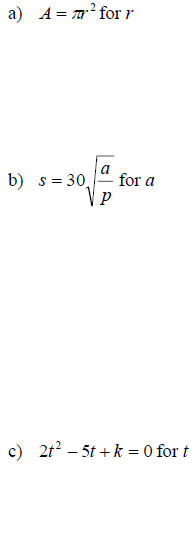
• Recall the Pythagorean Theorem,
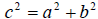
Example: A ladder is leaning against a house. The distance from the bottom of the ladder to the house is 5 ft. The distance from the top of the ladder to the ground is 1 ft less than the length of the ladder. How long is the ladder?
Example: A ball is projected upward from the
ground. Its distance in feet from the ground at t seconds is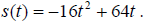
a) At what time will the ball hit the ground?
b) At what time will the ball be 32 ft from the ground?
Section 11.6: Graphs of Quadratic Functions
• We now look at how to graph quadratic equations
• In this section we look at horizontal shifts and vertical shifts associated
with parabolas
• We can also use a table of values to plot points and determine the graph of
quadratic equations
• A quadratic function is of the form ; standard form
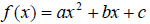
• A quadratic function can also be in the form of
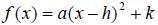
• Functions of the form 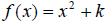 have a vertical shift
of k units up if k is positive and k units down if k is negative
have a vertical shift
of k units up if k is positive and k units down if k is negative
• Functions of the form 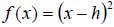 have a horizontal
shift of h units to the right if h is positive and h units to the left if h is
negative
have a horizontal
shift of h units to the right if h is positive and h units to the left if h is
negative
• Recall the ideas of domain and range; interval notation
• Recall the general shape of quadratic functions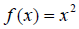
General Principles
1. Graph the quadratic function defined by 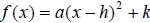 is a parabola with vertex
is a parabola with vertex 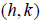
2. The graph opens up if a is positive and down if a is negative
3. The graph is wider than that of 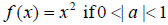 . The
graph is narrower than that of
. The
graph is narrower than that of 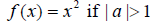
Examples: Graph the following functions. Use the ideas of vertical shift, horizontal shift and the general principles.
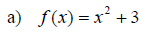
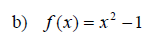
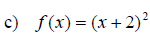
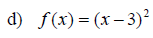
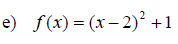
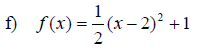
Section 11.7: More about Parabolas and Their
Applications
• We use a similar set of principles when graphing quadratic equations in
standard form
• To determine the vertex of the parabola , we use the following formula
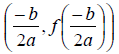
General Principles of a Quadratic Function in Standard
Form
1. Determine whether the graph opens up or down. If a>0 the parabola opens up.
If a<0 the parabola opens down.
2. Find the vertex using the vertex formula.
3. Find the x and y intercepts. Recall that an x intercept is found when y is
replaced with zero and the equation is solved for x. A y intercept is found when
x is replaced with zero and the equation is solved for y; this usually involves
factoring.
4. Graph the vertex and intercepts. Plot additional points as needed.
Example: Graph the given quadratic equation. Use the general principles as described above. Also, determine the domain and range.
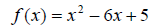
• We can use the vertex formula to solve applications of
quadratic equations
• Application problems which involve maximum or minimum areas require the use of
the vertex formula
Example: Use the vertex formula to solve the
following application problems.
1. A farmer has 100 ft of fencing. He wants to put a fence around the
rectangular field next to a building. Find the maximum area he can enclose and
the dimensions of the field when the area is maximized.
2. A toy rocket is launched from the ground so that its
distance in feet above the ground after t seconds is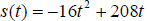 .
Find the maximum height it reaches and the number of seconds it takes to reach
that height.
.
Find the maximum height it reaches and the number of seconds it takes to reach
that height.
| Prev | Next |