Analyzing Matrices
Matrices can be used to organize all sorts of data, not just sales data. In
this investigation,
you will explore three different situations in which matrices are used to
help make sense of data.
Archeologists study ancient people and their cultures. One way they study
these people is by exploring sites where they have lived and analyzing objects
which they have made. Archeologists use
matrices to classify and then compare the
objects they find at various archeological
sites. For example, suppose that pieces of
pottery are found at five different sites. The
pottery has certain characteristics: it is either
glazed or not glazed, ornamented or not, colored
or natural, thin or thick.
1. Information about the characteristics of the
pottery at all five sites is organized in the
matrix below. A “1” means the pottery has
the characteristic and a “0” means it does
not have the characteristic.

Pottery Characteristics
| Glaze | Orn | Color | Thin | |
| Site A | 0 | 1 | 0 | 0 |
| Site B | 1 | 0 | 0 | 0 |
| Site C | 1 | 0 | 1 | 0 |
| Site D | 1 | 1 | 1 | 1 |
| Site E | 0 | 1 | 1 | 1 |
a. What does it mean for pottery to be “glazed”? “Ornamented”?
b. What does the “1” in the third row and the first column mean?
c. Is the pottery at site E thick or thin?
d. Which site has pottery that is glazed and thick, but is not ornamented or
colored?
e. How many of the sites had glazed pottery? Explain how you used the rows
or columns of the matrix to answer the question.
2. You can use the matrix to determine how much the pottery differs between
sites. For example, the pottery found at sites A and B differ on exactly two
characteristics—glaze and ornamentation. So you can say that the degree of
difference between the pottery at sites A and B is 2.
a. Explain why the degree of difference between pottery at sites A and C is
3.
b. Find the degree of difference between sites D and E.
3. You can build a new matrix that summarizes all the degree of difference
information.
a. What number would best describe the difference between site A and site A?
b. What number should be placed in the third row, fourth column? What does
this number tell you about the pottery at these two sites ?
c. Complete the degree of difference matrix shown below.
Degree of Difference
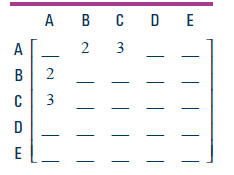
d. Describe at least one pattern you see in the degree of difference matrix.
4. Archeologists want to learn about the civilizations that existed at the
sites. For
instance, they would like to know whether different sites represent different
civilizations and whether one civilization was more advanced than another. A
lot of evidence is needed to make such decisions. However, make some conjectures
based just on the pottery data in the matrices from Activities 1 and 3.
a. Find two sites that you think might be from the same civilization. Explain
how the pottery evidence supports your choice.
b. Find two sites that you think might be from different civilizations. Give an
argument defending your choice.
c. Give an argument supporting the claim that the civilization at site D was
more advanced than the others. What assumptions are you making about
what it means for a civilization to be “advanced”?

5. Matrices also are used frequently by sociologists in their study of social
relations.
For example, a sociologist may be studying friendship and trust among
five classmates at a certain high school. The classmates are asked to indicate
with whom they would like to go to a movie and to whom they would loan $5.
Their responses are summarized in the following two matrices. (“1” means
“yes” and “0” means “no”.) Each matrix is read from row to column. For
example, the “1” in the first row and fourth column of the movie matrix means
that student A would like to go to a movie with student D.
Movie Matrix
| Would Like to Go to a Movie |
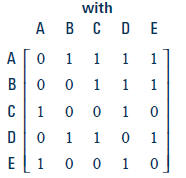 |
Loan Matrix
| Would Loan Money |
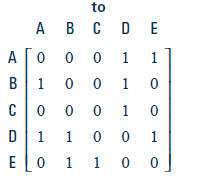 |
a. Would student Alike to go to a movie with student B? Would student B like
to go to a movie with student A?
b. With whom would student D like to go to a movie?
c. What does the “0” in the fourth row, third column of the loan matrix mean?
d. To whom would student A loan $5?
e. A square matrix has the same number of rows and columns. The main
diagonal of a square matrix is the diagonal line of entries running from the
top left corner to the bottom right corner. Why do you think there are zeroes
for each entry in the main diagonals of the matrices above?
6. Now consider further information conveyed by the matrices above.
a. Explain why the movie matrix could be used to describe friendship, while
the loan matrix could describe trust.
b. Write two interesting statements about friendship and trust among these
five students, based on the information in the matrices.
7. Discuss with your group how you can use the rows or columns of the movie
and loan matrices to answer the following questions.
a. How many students does student C name as friends?
b. How many students name student C as a friend?
c. Who seems to be the most trustworthy student?
d. Who seems to be the most popular student?
Checkpoint
In the previous investigations , you performed computations on the row or
column entries of a matrix to get useful information about the situation
being modeled. Give three examples from your analysis of pottery, shoe
sales, or friendship and trust showing how you operated on the entries of
the given matrix to get additional information . For each example, describe
the situation, the computation, and the information obtained.
Be prepared to share your group’s examples with the class.
On Your Own
In 2001, the University of Notre Dame won the NCAA women’s basketball
championship. They completed a 34-2 season by defeating Purdue University in
the championship game.
a. Senior Ruth Riley was the high scorer in the championship game for Notre
Dame, with 28 points. Teammate Erika Haney scored 13 points. What other
factors besides points scored should be taken into account when deciding
which player contributed most to the victory?
The matrix below shows some of the non-shooting performance statistics for the
seven Notre Dame players who played in the championship game.

Non-Shooting Performance Statistics
| Assists | Steals | Rebounds | Blocked Shots |
Turn-overs | Fouls | |
| Haney | 2 | 1 | 5 | 1 | 0 | 3 |
| Siemon | 6 | 0 | 9 | 0 | 7 | 3 |
| Riley | 1 | 0 | 13 | 7 | 3 | 3 |
| Ratay | 2 | 1 | 4 | 0 | 1 | 4 |
| Ivey | 4 | 6 | 5 | 1 | 4 | 0 |
| Joyce | 1 | 0 | 0 | 0 | 0 | 1 |
| Barksdale | 0 | 0 | 2 | 2 | 0 | 0 |
b. A “turnover” is when an action (other than fouling or scoring a basket)
gives
the other team control of the ball. How many turnovers did Ratay have?
c. What is a “rebound”? How many rebounds were made by the Notre Dame
players during the game?
d. Which of the performance factors do you think are positive, that is, they
contribute
toward winning the game? Which performance factors do you think are
negative? For the factors that are negative, change the entries in the matrix to
negative numbers .
e. Which player had the largest number of positive performance actions?
f. Describe how you could give a “non-shooting performance score” to each
player. The score should include both positive and negative factors. Which
player do you think contributed most to the game in the area of non-shooting
performance? Explain your choice.
Combining Matrices
You have seen that a matrix can be used to store and organize data. You also
have
seen that you can operate on the numbers in the rows or columns of a matrix to
get additional information and draw conclusions about the data. Sometimes it is
useful to combine matrices, as you will see in the next two situations.
1. Shown below are the movie and loan matrices you analyzed in the previous
investigation. Study both matrices to see how friendship and trust are related
in this group of five students.
Movie Matrix
| Would Like to Go to a Movie |
 |
Loan Matrix
| Would Loan Money |
 |
a. Who does student A consider friends and yet does not trust enough to
loan $5?
b. Do you think it is reasonable that a student could have a friend who he or
she does not trust enough to loan $5?
c. Who does student B trust and yet does not consider them to be friends? Do
you know someone who you trust but who is not a friend?
d. Who does student D trust and also consider to be friends?
2. A friend you trust is a trustworthy friend.
a. Combine the movie and loan matrices to construct a new matrix that shows
who each of the five students considers to be a trustworthy friend.
b. Write down a systematic procedure explaining how to construct the
trustworthy-friend matrix.
c. Compare your procedure with that of other groups.
d. Write two interesting observations about the information in this new matrix.
In the next situation, you will explore other ways of combining matrices and
learn
some of the ways in which matrix operations are used in business and industry.

In accordance with demand from American consumers, the Big Three automakers
in the U.S.—General Motors, Ford, and Chrysler—have been producing
many small cars. The matrices below show the production data for 1998 and
1999. Data are given in hundred thousands of small cars produced each quarter
(a quarter is three months).
1998 Small Auto Production
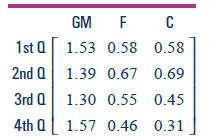
1999 Small Auto Production
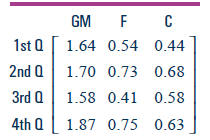
3. Analyze the two matrices above.
a. How many cars are represented by the first entry in the matrix for 1998?
b. According to these data, how many small cars were produced by Chrysler
in the second quarter of 1999?
c. Explain the meaning of the entry in the third row and second column of the
1998 matrix.
4. Additional information can be derived by combining the two matrices.
a. According to these data, by how much did first-quarter, small-car production
increase for GM from 1998 to 1999?
b. Construct a new matrix with the same row and column labels that shows
how much small-car production increased from 1998 to 1999 for each quarter
and each manufacturer. Explain any trends or unusual entries.
5. Suppose that the auto industry projected a 10% increase in small-car
production
from 1999 to 2000, over all quarters and all manufacturers. Construct a
matrix that shows the projected 2000 production figures for each quarter and
each manufacturer, based on the data given.
6. Construct a matrix with the same row and column labels as the given
matrices
that shows the total number of small cars produced over the two-year period
1998–99.
Checkpoint
In this investigation, you explored how combining two matrices or multiplying
each entry of a matrix by a number helped to derive new information.
a Which of the activities about small-car production involved
combining
matrices by adding corresponding entries?
b Which of the activities about small-car production involved combining
matrices by subtracting corresponding entries?
c Which of the activities about small-car production involved multiplying
each entry of a matrix by a number?
d Consider all the situations you have analyzed so far. What other
operations
have you performed on matrices?
Be prepared to explain your group’s selections to the
entire class.
Several of the operations you have performed on matrices in this
investigation
are commonly used and have been given standard names. To add matrices
means to combine them by adding corresponding entries. Thus, when adding two
matrices you add the entry in the first row and first column from one matrix to
the entry in that same position in the other matrix, and then do likewise for
the
entries in each of the other positions. If A represents one matrix and B
represents
another matrix, then A + B represents the matrix found by adding the matrices
entry by entry. Subtracting matrices (A – B) is just like adding matrices,
except
you subtract the corresponding entries instead of adding them. Multiplying a
matrix, B, by a number, k, means to multiply each entry in the matrix by that
number and is represented by kB.
On Your Own
Below are two matrices showing the 1999 and 1998 passing statistics for three
top NFL quarterbacks. (“Att” is an abbreviation for “passes attempted”; “Comp”
refers to passes completed; “TD” refers to passes thrown for a touchdown; and
“Int” refers to passes that were intercepted .)

1999 Passing Statistics
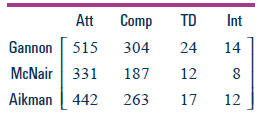
1998 Passing Statistics
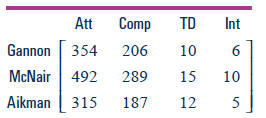
Let A represent the 1999 matrix and B represent the 1998 matrix.
a. Compute A + B. What does A + B tell you about the passing performance of
the three quarterbacks?
b. Compute A – B. What does A – B tell you about the passing performance of
the three quarterbacks?
c. Compute B – A.
•How do the numbers in B – A differ from the numbers in A – B?
•What does a negative number in the TDs column of A – B tell you about the
trend in touchdown passes from 1998 to 1999?
•What does a negative number in the TDs column of B – A tell you about the
trend in touchdown passes from 1998 to 1999?
d. Compute 1/2A. What could 1/2A mean for this situation?
| Prev | Next |