Beginning Algebra Departmental Review Sheet
[ Additional Content Outcome 7 (c), Sec 4.4, 4.5, 4.6]
Perform the indicated operations. (Also see problem 49)
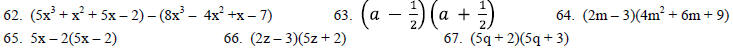
[Additional Content Outcome 7 (d), Sec 5.1, 5.2, 5.3, 5.4,
Summary Exercises on Factoring ]
Factor completely.
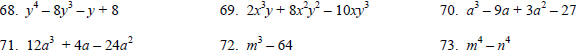
[Additional Content Outcome 7 (e), Sec 5.5, 6.6]
Solve
each equation. Show that the solutions check(s).
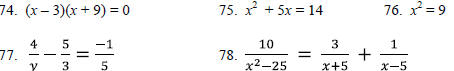
[Additional Content Outcome 7 (f), Sec 6.1, 6.2, 6.4, 6.5]
Perform the indicated operations and simplify if possible.
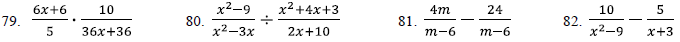
Simplify .
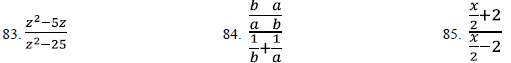
[Additional Content Outcome 7 (g), Appendix A pp 992-994,
p 214, p 218, p 226, p 231]]
Evaluate each of the following on a TI-82/83/84, if
possible. State the result the calculator shows exactly.
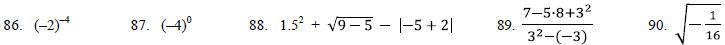
91. Find the quotient, if possible on a TI-82/83/84. State the full result the calculator shows exactly.
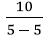
[Additional Content Outcome 7 (g), Appendix A pp 992-994,
p 214, p 218, p 226, p 231]
Graph these equations on a TI-82/83/84. Do all the
following as part of that process.
a) State your grapher model number
(TI-82/83/84, etc.).
b) For each equation – state all keystrokes used to enter
that function in the 
.
State precisely the sequence of keystrokes that
you use as directed in each part below. Write each separate keystroke
in a
separate box in a table similar to the one shown in the example.
Example: If
entering 
, the keystrokes (left-to-right) would be
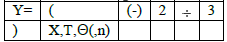
c) State how you view a basic centered (“standard”) graph
of any equation (once).
d) If in a “lecture” or hybrid section, you may be asked
to show your instructor the graph while it’s displayed on your
grapher. In any
section format, you may also be asked to sketch the graph you see displayed
either roughly or
carefully.
(Note: You may need to solve for y = mx + b form
first.)
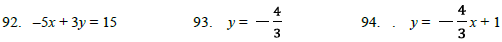
[Other problem types which are highly likely to appear on final]
[ Linear Inequalities in One Variable , Sec 2.8]
95. Solve the inequality.
Write the solution set in interval notation and graph it (on a number line). 3y
– 5 > 7y + 3
[Slope and Line concepts , Sec 3.3, 3.4]
96. Find the slope of the
line through the pair of points: (–1, –2) and (2, 4). 97. Find the slope and
y-intercept. –5x + 3y = 15
98. Determine whether the two lines are parallel,
perpendicular, or neither parallel nor perpendicular. (Graphing is not
sufficient. Use
algebra.)
3x – 2y = 6
2x + 3y = 3
[Other Polynomial Concepts :
Definitions and Division, Sec 4.4, 4.7]
99. Find the terms, coefficents and
degree of each term, and the degree of the polynomial, and tell whether the
polynomial is
a monomial , binomial, trinomial, or none of these: 4xy2 + 7xy +
9x3yz
100. Perform the division (using long division).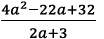
Verifying solutions: Sec 2.1, 2.2, 2.3, 2.8, 3.1, 5.5,
6.6]
Check all solutions in # 1-4, 72-76 + do the following:
101. True or false
(show a reason) :…5 is a solution of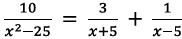 
.
[Model any problem using algebraic process - continued, p
38, p 44, 2.5, 2.8, 4.4, 4.5, 5.7, 6.6, 6.7]
* If it’s not a formula-based
problem, solve, showing all the steps: i) Read the problem, ii) Assign (Label
the unknown: x
represents what words, develop a verbal model), iii) Write an
equation, iv) Solve, v) State the answer (as a compete
sentence), vi) Check
(makes sense?).
* If it is a formula-based problem (e.g., #’s 106 & 107) show
your replacement step and all work. Write the final answer as a
complete
sentence.
102. (2.5) On March 17, 2005, a new record was set for the world’s
largest sandwich. The fillings of this sandwich were
corned beef, cheese,
lettuce, and mustard. The sandwich, made by Wild Woody’s Chill and Grill in
Roseville, Michigan,
was 12 ft long, 12 ft wide, and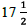 
in. (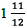
ft) thick. What
was the volume of the sandwich? (Source: Guinness World
Records.)
103. (2.8) Mabimi Pampo has scores of 96 and 86 on his first two geometry tests. What
possible scores can he make on his
third test so that his average is at least
90?
[Model any problem using algebraic process - continued, p
38, p 44, 2.5, 2.8, 4.4, 4.5, 5.7, 6.6, 6.7]
104. (4.4) If an object is
projected upward under certain conditions, its height in feet is given by the
trinomial
–16x2 + 60x + 80, where x is in seconds. Evaluate this polynomial for
2.5, and then use the result to fill in the blanks:
If 
seconds have elapsed, the
height of the object is feet.
105. (5.6) If an object is projected upward from
ground level with an initial velocity of 64 ft per sec, its height h in t
seconds
later is h = –16t2 + 64t. After how many seconds does the object hit the
ground?
106. (5.6) The area of this rug is 80 sq. units. Find its length and width.
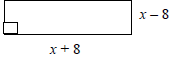
107. (6.7) A pump can pump the water out of a flooded
basement in 10 hr. A smaller pump takes 12 hr. How long will it take
to pump the
water from the basement with both pumps? (State the answer exactly.)
108. (6.7)
A boat can go 20 mi against a current in the same time that it can go 60 mi with
the current. The current is 4 mph.
Find the speed of the boat in still water.
[Geometric Concepts]
109. (4.4) Find a polynomial that represents the perimeter
of the triangle.
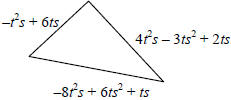
110. (4.5) Find a polynomial that represents the area of the shaded region in the figure.
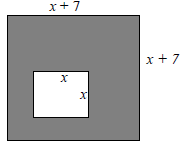
| Prev | Next |