| |
Course Goals
We will learn to:
 Solve linear and quadratic equations
and inequalities Solve linear and quadratic equations
and inequalities
 Graph lines, circles, and parabolas Graph lines, circles, and parabolas
 Graph inequalities Graph inequalities
 Apply linear , quadratic, and other
models to solve problems Apply linear , quadratic, and other
models to solve problems
 Use exponential and logarithmic
functions Use exponential and logarithmic
functions
 Count Count |
| Required Materials
You will need
 the book the book
Jerome E. Kaufmann, College Algebra, 6/e
 a calculator a calculator
At minimum, your calculator should have
 arbitrary exponents arbitrary exponents
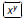 or or
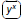
 exponentials exponentials
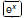
 logarithms logarithms
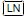
 factorials factorials
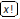
 permutations permutations
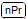
 combinations combinations
 |
Your Grade
 Weekly homework — 15% Weekly homework — 15%
 Problems listed in syllabus Problems listed in syllabus
 Each week’s problems due the
following Wednesday Each week’s problems due the
following Wednesday
 6–8 problems graded 6–8 problems graded
 Three hour exams — 15% each = 45% Three hour exams — 15% each = 45%
 Final exam — 40% Final exam — 40% |
| Classroom Expectations
 Attend class Attend class
 Not mandatory Not mandatory
 No attendance points or
participation points No attendance points or
participation points
 A good deal of lecture material will
not be in the slides A good deal of lecture material will
not be in the slides
 Do not make yourself a distraction Do not make yourself a distraction
 No loud conversations No loud conversations
 No newspaper rustling No newspaper rustling
 No stinky or noisy food No stinky or noisy food
 Most importantly, ask questions! Most importantly, ask questions! |
Outline
 Review of Basic Concepts Review of Basic Concepts
 The Real Numbers The Real Numbers
 Fractions Fractions
 Integer Exponents Integer Exponents
 Positive Integer Exponents Positive Integer Exponents
 Zero as an Exponent Zero as an Exponent
 Negative Integer Exponents Negative Integer Exponents
 Scientific Notation Scientific Notation
 Radicals Radicals
 Definition and Notation Definition and Notation
 Simplest Radical Form Simplest Radical Form
 Fractional Exponents Fractional Exponents |
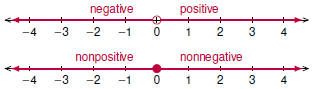
The Real Numbers
Integers
 |
The Real Numbers
RationalsThe
rationals are the set of all possible quotients formed using
integers
 A rational number can be written as A rational number can be written as
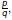 where p and q are where p and q are
integers with 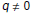
 A rational number can also be
written in decimal form, and will A rational number can also be
written in decimal form, and will
either terminate
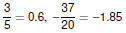
or repeat
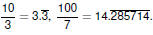
|
The Real Numbers
Completing the Reals
Irrational numbers cannot be expressed as fractions. This means
they have decimal representations that neither terminate nor
repeat.
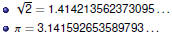
The reals are difficult to define. For now, let’s just say the reals
comprise the rationals and the irrationals. |
Fractions
Simplifying Fractions
We can simplify fractions by canceling the same thing
from the
numerator and the denominator.
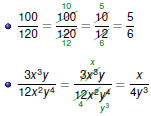
|
Fractions
Arithmetic with Fractions
To add or subtract fractions , get a common
denominator, and then
add or subtract the numerators.
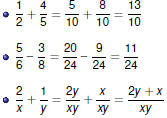
|
Fractions
Arithmetic with Fractions
To multiply fractions , multiply the numerators and
denominators
separately. Cancel first if possible.
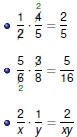 |
Fractions
Arithmetic with Fractions
To divide fractions, multiply by the reciprocal of
the divisor .
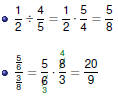
|
Positive Integer Exponents
Terminology and Notation
|
Integer exponents denote repeated multiplication |
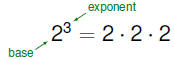
 The base is
repeatedly multiplied by itself The base is
repeatedly multiplied by itself
 The exponent
indicates the number of factors The exponent
indicates the number of factors
Nitpick
An exponent does not indicate the “number of times the base is
multiplied by itself” |
|
Positive Integer Exponents
First Definition of bn
Definition
For any positive integer n and any real number b,
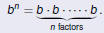 |
|
Positive Integer Exponents
Properties of Exponents
Properties of Exponents
For any positive integers m and n, and for any real numbers a
and
b,
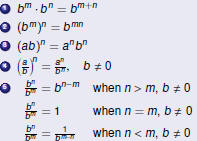 |
|
Zero as an Exponent
What Should a Zero Exponent Mean?
Zero exponents should satisfy the same properties as
positive
exponents. Let m = 0 in Property 1:
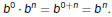
So, unless b is zero, b0 must be 1.
Definition
For any nonzero real number b,
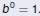 |
|
Negative Integer Exponents
What Should a Negative Exponent Mean?
Again, we want negative exponents to satisfy the same
properties
as positive exponents. Set m = −n in Property 1:
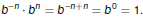
So b-n must be the reciprocal of bn.
Definition
For any positive integer n and any nonzero real number b,
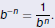 |
|
Negative Integer Exponents
Restating the Properties of Exponents
Properties of Exponents
For any integers m and n, and for any real numbers a and b,
 |
|
Scientific Notation
Scientific Notation
Definition
A real number written in the form
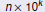 or or
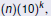
with 1 ≤n < 10 and k an integer, is in
scientific notation. |
To write a number in scientific notation,
 Move the decimal point to the immediate right of the first Move the decimal point to the immediate right of the first
nonzero number—this produces n
 Count the number of places the decimal point moved—this Count the number of places the decimal point moved—this
gives you |k|
 If you moved the decimal point to the left, k is positive; if you If you moved the decimal point to the left, k is positive; if you
moved it right, k is negative. |
Examples
Examples
 Evaluate Evaluate
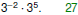
 Evaluate Evaluate
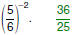
 Simplify Simplify
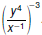 . Use only nonnegative exponents. . Use only nonnegative exponents.
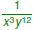
 Express 0.000000078 in scientific
notation. Express 0.000000078 in scientific
notation. 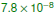
 Use scientific notation to evaluate Use scientific notation to evaluate
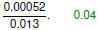 |
Definition and Notation
Definition of
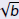 The book’s definition is wrong!
Definition
For any nonnegative real number a,
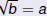 if and only if if and only if
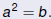 |
Note: Even though
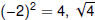 is 2, not −2. is 2, not −2.
For any real number b, if
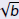 exists, it is nonnegative. exists, it is nonnegative. |
|
Definition and Notation
Definition of
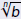
Definition
For any positive integer n and nonnegative real number a,
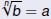 if and only if if and only if
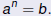
If n is odd, this holds for any (possibly negative) real number
a. |
Examples
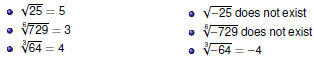
|
Simplest Radical Form
Properties of Radicals
Notice that there is no property for
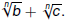 A sum of radicals A sum of radicals
generally cannot be simplified.
Also notice how similar these properties are to the properties of
exponents. . |
Simplest Radical Form
Simplest Radical Form
Definition
An expression is said to be in simplest radical form if:
 No fraction appears within a radical sign .
No fraction appears within a radical sign .
 No radical appears in the denominator.
No radical appears in the denominator.
 No radicand contains a factor that is a perfect power of the
No radicand contains a factor that is a perfect power of the
index. |
An example of the last condition is
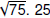 is a factor of 75, and is a factor of 75, and
25 is a perfect square .
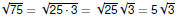
|
Simplest Radical Form
Rationalizing the Denominator
To clear a radical from the denominator, multiply the numerator and
the denominator by a radical that will allow you to remove the
radical sign.
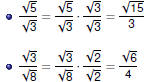
In case there is a sum ( or difference ) of radicals
in the
denominator, say 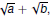 multiply by the
conjugate multiply by the
conjugate 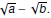 |
Examples
Examples
 Express Express
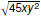 in simplest radical form. in simplest radical form.
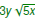
 Express Express 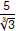 in simplest radical form. in simplest radical form.
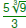
 Rationalize the denominator and simplify Rationalize the denominator and simplify
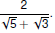
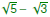
 Rationalize the denominator and simplify Rationalize the denominator and simplify
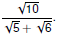
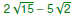
|
Roots are Exponents !
The nth root of b
Recall that 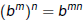 . Suppose m = 1/n. Then . Suppose m = 1/n. Then
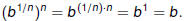
So 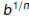 is the nth root of b. is the nth root of b.
Definition
For any positive integer n and any real number b, if
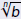 exists, then exists, then
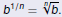 |
|
Roots are Exponents!
Definition of
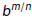
Because 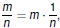 we have we have
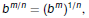
and
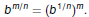
Definition
For any positive integer n and any real number b, if m/n is a
rational number written in lowest terms, and if
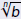 exists, then
exists, then
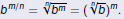 |
|
Examples
Examples
 Evaluate Evaluate 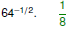
 Evaluate Evaluate 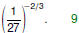
 Evaluate Evaluate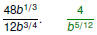
 Express Express 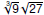 in simplest radical form.
in simplest radical form.
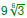
 Simplify Simplify 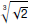 into one radical.
into one radical.
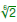
|
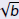
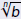
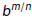

 arbitrary exponents
arbitrary exponents
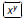 or
or
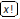
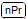

 Review of Basic Concepts
Review of Basic Concepts Integer Exponents
Integer Exponents Radicals
Radicals Fractional Exponents
Fractional Exponents
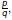 where p and q are
where p and q are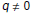
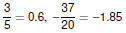
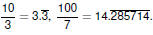
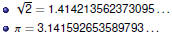
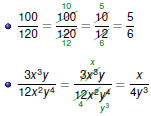
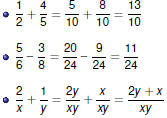
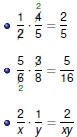
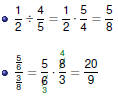
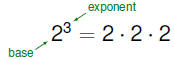
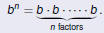
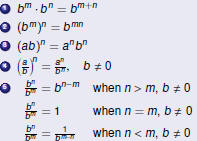
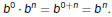
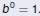
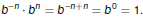
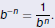

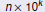 or
or
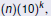
 Evaluate
Evaluate
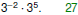
 Evaluate
Evaluate
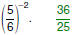
 Simplify
Simplify
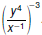 . Use only nonnegative exponents.
. Use only nonnegative exponents.
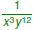
 Express 0.000000078 in scientific
notation.
Express 0.000000078 in scientific
notation. 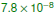
 Use scientific notation to evaluate
Use scientific notation to evaluate
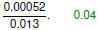
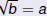 if and only if
if and only if
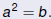
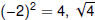 is 2, not −2.
is 2, not −2.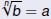 if and only if
if and only if
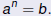
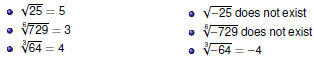
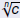 are real numbers, then
are real numbers, then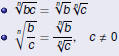
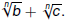 A
A 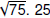 is a factor of 75, and
is a factor of 75, and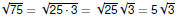
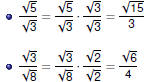
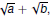 multiply by the
conjugate
multiply by the
conjugate 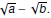
 Express
Express
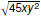 in simplest radical form.
in simplest radical form.
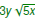
 Express
Express 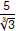 in simplest radical form.
in simplest radical form.
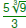
 Rationalize the denominator and simplify
Rationalize the denominator and simplify
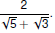
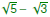
 Rationalize the denominator and simplify
Rationalize the denominator and simplify
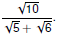
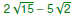
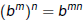 . Suppose m = 1/n. Then
. Suppose m = 1/n. Then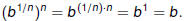
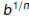 is the nth root of b.
is the nth root of b.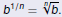
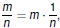 we have
we have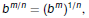
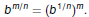
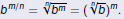
 Evaluate
Evaluate 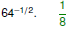
 Evaluate
Evaluate 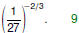
 Evaluate
Evaluate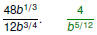
 Express
Express 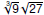 in simplest radical form.
in simplest radical form.
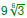
 Simplify
Simplify 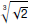 into one radical.
into one radical.