Completing the Square

To complete the square for the expression x² + bx , add 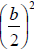, which is the square of
half the coefficient of x . Consequently,

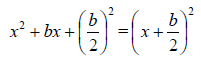
When solving quadratic equations by completing the square, you must add 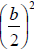to both
sides to maintain equality.

Completing the Square: Leading Coefficient is 1

Let’s solve the equation x ² − 6x + 2 = 0 by completing the square.

x2 + 6x + 2 = 0	Original Equation
x2 + 6x = −2	Subtract 2 from both sides
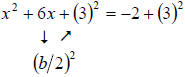	Divide the 6 by 2, square it, and then add to both sides
x2 + 6x + 9 = 7	Simplify
(x + 3)2 = 7	Perfect square trinomial
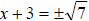	Extract square roots
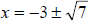	Solutions

Completing the Square: Leading Coefficient is Not 1

Let’s solve the equation 3x² − 4x − 5 = 0 by completing the square.

If the leading coefficient of a quadratic equation is not 1, you should divide both sides of
the equation by this coefficient before completing the square.

3x2 − 4x − 5 = 0	Original equation
3x2 − 4x = 5	Add 5 to both sides
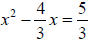	Divide both sides by 3
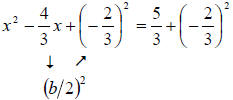	Divide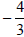 by 2, square it, and then add to both sides
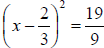	Perfect square trinomial
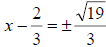	Extract square roots
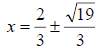	Solutions

Using a graphing calculator , you can see that the two solutions are approximately
2.11963 and –0.78630, which agree with the two graphical solutions shown below.

Completing the Square: One Term is Not Present

Let’s solve the equation 4x² − 7x = 0 by completing the square.

As you can see, we have no constant but we will treat the problem the same as if there
was a constant present . We skip the step of moving the constant over to the other side of
the equation and continue on from there.

4x2 − 7x = 0	Original equation
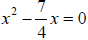	Divide both sides by 4
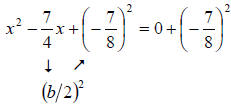	Divide 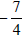by 2, square it, and then add to both sides
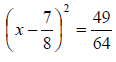	Perfect square trinomial
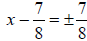	Extract square roots
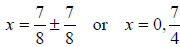	Solutions