Estimating with Fractions
NYS Mathematics, Science, and Technology Learning
Standards Addressed
Standard 1: Students will use mathematical analysis, scientific inquiry, and
engineering
design, as appropriate, to pose questions, seek answers, and develop
solutions .
Standard 3: Students will understand mathematics and
become mathematically confident
by communicating and reasoning mathematically, by applying mathematics
in real -world settings, and by solving problems through the integrated study
of number systems , geometry, algebra, data analysis, probability, and
trigonometry .
Standard 6: Students will understand the relationships and
common themes that connect
mathematics, science, and technology and apply the themes to these and
other areas of learning.
Standard 7: Students will apply the knowledge and thinking
skills of mathematics,
science, and technology to address real-life problems and make informed
decisions.
Objectives:
• The student will be able to estimate sums, differences, products, and
quotients involving
fractions and mixed numbers (Knowledge).
• The student will be able to explain the process of estimating fractions and
mixed numbers
to someone unfamiliar with the concept (Comprehension).
Materials:
• PowerPoint Presentation (“7.1 Estimating with Fractions”)
• Computer with Microsoft PowerPoint (and the ability to project what is on the
computer
onto a larger screen).
• One “Estimating Fractions – FAQ” note sheet for each student (20 total).
• One “Estimating Fractions – Homework” sheet for each student (20 total).
Anticipatory Set:
When students enter the room, have the first slide of the PowerPoint
Presentation titled “7.1
Estimating with Fractions” (included with this lesson plan) projected onto the
front screen. This
slide gives today’s lists today’s Agenda and includes a Far Side comic to
lighten the mood at the
beginning of class.
Once everyone is seated, click to the next slide
(“Warm-Up”). This slide instructs the students to
write a short paragraph in their math journals explaining how they would explain
to someone the
process of estimating the numbers 59.6541, 4.302, and 77.77777 to the nearest
tenth. Give
students between 3-5 minutes to complete this task, and then ask, “Can someone
volunteer to
read what he or she has written for the class?” (Responses should explain that
59.6541 would be
rounded to 59.7, because the digit in the hundredths place is a 5, and the rule
for rounding
numbers is to round up if this digit is 5 or higher and round down otherwise.
Using this
reasoning, 4.302 would be rounded to 4.3 and 77.77777 would be rounded to 77.8.)
Say, “Today, we are going to devise a rule somewhat
similar to this for estimating fractions and
mixed numbers.”
Lesson Body:
Hand out one “Estimating Fractions – FAQ” note sheet to
each student. Ask everyone to fill in
this sheet as we cover today’s lesson. (All answers appear in the PowerPoint
presentation.) Click
the PowerPoint presentation to the next slide (slide 3). The first question from
the note sheet
should appear on the screen, “Why would we want to know how to estimate
fractions?” Give
students a change to suggest an answer of their own, and then click the mouse
button to reveal
the response “to quickly estimate the sum, difference, product , or quotient of
an expression
involving fractions or mixed numbers.” (Throughout this lesson, students should
be writing the
words written in italics on their note sheet.)
Next, pose the question “When am I ever going to need to
estimate fractions?” Click the mouse
button three times to reveal the first three responses (Approximating the amount
of ingredients
needed in a recipe, Estimating the amount of money you will make doing a job,
Estimating the
distance between two locations ). Clicking the mouse button one more time will
reveal “Any
other ideas?” in which the floor should be open to the students for any
additional examples they
may have.
Move on to the next slide by clicking the mouse button.
This slide (4) corresponds with the next
bullet on the note sheet: “To estimate the sum or difference of fractions, round
each fraction
to…” Clicking the mouse button twice will reveal the answer: 0, ½, or 1,
whichever is closest.
After students have had a chance to write this down, click on to slide 5 to
answer the next
question, “How do you decide what to round to?” Clicking the button again
reveals “Drawing
fraction models can help you decide how to round.” Example A illustrates this
technique. Click
the mouse button again to reveal the example of rounding 5/8 that is already
printed on the
students’ note sheets. Show that the white bar is divided into 8 even pieces,
and that five of these
pieces have been filled in blue to represent 5/8. Notice that 0, ½, and 1 are
also clearly marked
on this bar, and ask students, “Is the end of the blue bar closest to 0, ½, or
1?. (Students should
see that 5/8 is closet to ½, and should write this answer in the appropriate
line on their note
sheet.) Clicking the mouse button again also reveals this answer.
Click to the next slide (6), and then click the mouse
button two more times to reveal the
cautionary note: “It is deceiving what to round some fractions to, so if you
ever have any doubt,
draw the fraction models to help you.” Clicking the mouse button three more
times reveals
Example B: “What would you round 1/3 to?” As before, a fraction model has been
drawn on the
PowerPoint screen, (but it has been left for the students to draw in their
notes). Show students
that in this case, although their first instinct may be to round this fraction
to 0, the blue bar is
actually closer to ½ than 0. Click the mouse button again to show the answer:
1/3 should be
rounded to ½.
Click to the next slide (7) for Example C. Explain that
this question, What would you round 2/3
to, is also deceiving. Click the mouse two times to reveal the question. Say,
“Your instinct may
be to round 2/3 to 1, but if we take a look at the fraction model, we find that
this is not the best
answer.” (Click the mouse again to reveal the fraction model). Show students
that this time, the
blue bar is actually closer to ½ than 1. Click the mouse one more time to reveal
the answer: ½.
Move on to slide 8 – “Activity.” Allow students to work
with the person they’re sitting next to
and estimate each of the fractions listed on the screen (which are also printed
on their sheet) to 0,
½, or 1 and place them in the appropriate column in the table on their note
sheet. Give students
between 5 and 10 minutes to complete this, and then go around the class asking
the pairs what
they estimated each fraction to, beginning with 1/5 and proceeding through 5/6.
(Each time, after
a pair gives their answer, click the mouse button once and the fraction will
slide down to its
correct column in the table on the screen.)
Click on to slide 9 – which gives students one more
essential note before bringing the lesson to a
close: “What about Mixed Numbers?” Explain “when we are asked to estimate mixed
numbers,
we use a similar process. The mixed number can either be rounded down the whole
number that
appears in the mixed number, the “½ of the mixed number” or one greater than the
whole
number that appears in the mixed number.” Example D illustrates this: 7 ¼ can
either be rounded
to (a) 7 , (b) 7 ½ , or (c) 8. Ask students “Can anyone tell me why estimating
this mixed number
is especially difficult?” (Students should say that 7 ¼ falls directly between 7
and 7 ½.) Say,
“Numbers like this are somewhat ambiguous to round. In this case, it is
acceptable to either
round down to 7 or round up to 7 ½.”
Closure:
The next slide, (10) contains the essential question for
this lesson, which students are again asked
to respond to in a brief paragraph written in their journal. (Allow about 5
minutes for this).
(1) Summarize what you learned about estimating fractions and mixed numbers today.
(Responses should include that fractions can be estimating
by either rounding them to 0, ½, or 1,
and a similar procedure is used when rounding mixed numbers. Mention should also
be made of
using fraction models to help decide which of these the number should be rounded
to. Other
responses are possible as well.)
If time permits, ask a student or two to volunteer what
they have written. Lastly, click to the last
slide (11) which lists the homework assignment. Pass out the sheet labeled
“Homework: 7.1
Estimating with Fractions” to each student.
Accommodations for IEP:
Since this lesson is essentially uses a direct teaching
method of instruction , the student with
ADD may have a particularly difficult time focusing. Remind the student before
class that he is
expected to complete all notes and activities that are contained within today’s
lesson, but if he
feels like he needs to get up and stretch once or twice during the period, he
may do so quietly.
Homework/Assessment
The homework worksheet (7.1 Estimating with Fractions)
essentially reviews the concepts
presented in the PowerPoint presentation, as well as taking the lesson a step
further. Students are
first asked to round fractions to 0, ½, or 1 (as they did in the class activity)
as well as estimating
the mixed numbers, as shown in the lesson. After this, they are asked to use
this knowledge to
estimate some algebraic expressions by first estimating the fractions and mixed
numbers
contained within them. Finally, students are presented with a real- life
scenario in the form of a
word problem that uses the techniques from today’s lesson.
Extensions
If time permits, have students do exercises 16-43 on page
270 of their textbook orally. These
problems ask them to round fractions or estimate expressions involving
fractions. By having
them practice doing these orally, they will gain practice for the homework and
also see the
relevance of estimating with fractions. (It allows them to evaluate otherwise
difficult expressions
quickly.)
Estimating Fractions - FAQ
• Why would we want to know how to estimate fractions?
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
• When am I ever going to need to estimate fractions?
1) _____________________________________________________________________
2) _____________________________________________________________________
3) _____________________________________________________________________
4) _____________________________________________________________________
• To estimate the sum or difference of fractions, round each fraction to
____, ____, or ____.
• How do you decide what to round to?
__________________________________________________________________________
__________________________________________________________________________
Example A:

Is 5/8 closest to 0, 1/2, or 1? ________
Caution!!!
• It is deceiving what to round some fractions to, so if
you ever have any doubt …
__________________________________________________________________________
Example B:
What would you round 1/3 to? ________
Example C:
What would you round 2/3 to? ________
Activity:
Estimate each of the fractions below to whichever is closest and place them in
the appropriate
column in the table that follows.
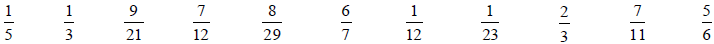
| Fractions Close to 0 | Fractions Close to 1/2 | Fractions Close to 1 |
What About Mixed Numbers?
• We can follow a similar procedure for estimating mixed
numbers.
Example D:
What would you round 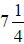 to?
to?
(a) 7 (b) 7 ½ (c) 8
 Round each fraction to 0, 1/2, or 1:
Round each fraction to 0, 1/2, or 1:
(1) 1/6______ (2) 3/5 ______ (3) 9/10 ______ (4) 3/10 ______
(5) 2/7 ______ (6) 1/4 ______ (7) 7/50 ______ (8) 10/13 ______
 Estimate each mixed number:
Estimate each mixed number:
(9) 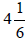 ______ (10)
______ (10)
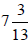 _______ (11)
_______ (11)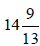 _______
(12)
_______
(12) 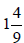 ______
______
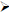 Estimate each expression by first estimating
the fractions and then adding the
Estimate each expression by first estimating
the fractions and then adding the
estimations.
Example: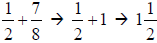


 Answer the following question:
Answer the following question:
Komodo dragons are the largest lizards ever to have lived. A 250-point
komodo dragon can eat
enough in one sitting to increase its weight by 3/4. Estimate 3/4 x 250 to find
how much weight a
komodo dragon would gain after eating.
| Prev | Next |