Rational Expressions
Operations with Rational Expressions
The operations of addition, subtraction, multiplication, and division with
rational expressions follow the same
rules that are used with common fractions. The key, as with simplifying rational
expressions, is to factor the
polynomials .
I. Multiplication of Rational Expressions
Recall with fractions 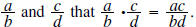 Also recall when mulitplying fractions that you may
Also recall when mulitplying fractions that you may
cross-cancel; that is, reduce common factors of any numerator with any
denominator.
Example 1:
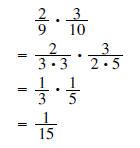
The same is true of multiplying rational expressions. As before, the key is to factor the polynomials first.
Example 2: Simplify
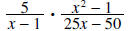
Solution : First factor the polynomials. Don’t forget to cancel common factors!
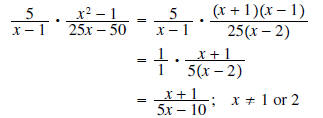
Before looking at the next example, recall our strategies
for factoring:
1. Factor out any common factors
2. If more than 3 terms, try factoring by grouping
3. Recognize special products
4. Factor trinomials using product /sum strategies:
a) 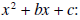 factors into (x+m)(x+n) where
factors into (x+m)(x+n) where
mn=c and m+n=b
b) 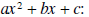 split bx into mx+nx, where
split bx into mx+nx, where
mn=ac and m+n=b, then factor by grouping.
Example 3: Simplify
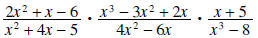
Solution:
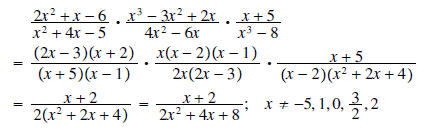
Example 4: Simplify
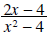
Solution:
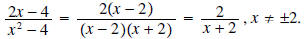
II. Division of Rational Expressions
Recall with fractions 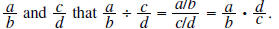 In other words, dividing by a fraction is the
In other words, dividing by a fraction is the
same as multiplying by its reciprocal. The same is true for rational
expressions. As before, the key to making
the work easier is to factor the polynomials first.
Example 5:
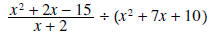
Solution: Begin by writing the second term as
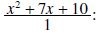
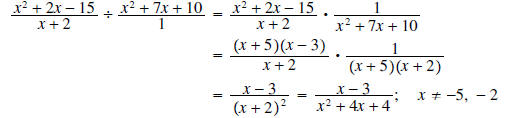
Notice that the x+2 terms cannot be cancelled since both are in the denominator.
Multiplication and Division can also appear together. Only
take the reciprocal of the fractions you are
dividing.
Example 6:
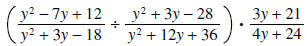
Solution: We only take the reciprocal of the second fraction:
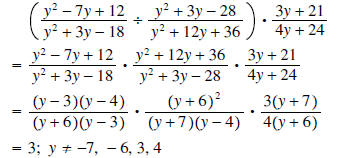
Question: Explain why the values -7, -6, 3, and 4
are excluded in the previous example.
Answer: The easiest way to understand why these values have been excluded is to
write
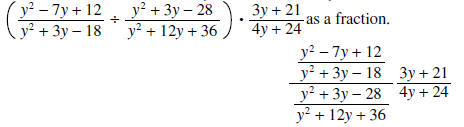
y≠-6 follows since 4y+24 cannot equal 0.
We also get y≠3 because the term
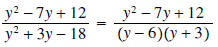
The next observation is that the denominator of
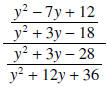
that is,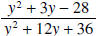 cannot equal
zero. Factoring the numerator and denominator of this rational expression
cannot equal
zero. Factoring the numerator and denominator of this rational expression
we have
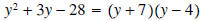
The numerator is zero if y =-7 or if y=4. This accounts for
excluding the numbers -7 and 4. The
denominator of
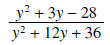
factors into 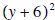 which
means we have to exclude -6, but we have already done that.
which
means we have to exclude -6, but we have already done that.
Question: What values of x are not allowed in the rational expression
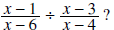
Answer: 3, 4, 6 (The value 3 is not allowed because
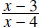 is zero at x=3 and we cannot divide by 0.
is zero at x=3 and we cannot divide by 0.
x=4 is not allowed because we have the term x-4 in the denominator. Similarly
x=6 is not allowed
because the term x-6 is the denominator of 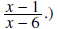
III. Addition and Subtraction of Rational Expressions
Recall that addition and subtraction is done by first
finding a common denominator. The least common
denominator (LCD) of several fractions is the product of all prime factors of
the denominators. A factor only
occurs more than once in the LCD if it occurs more than once in any one
fraction. Once you have the LCD,
convert each fraction to an equivalent fraction with the LCD, then add or
subtract the numerators.
Example 7:
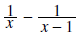
Solution: The LCD here is
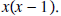 We convert each fraction to an equivalent
one with this
We convert each fraction to an equivalent
one with this
denominator: That is,
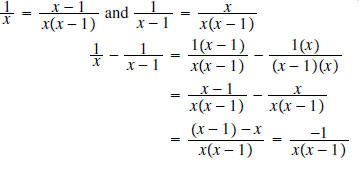
Example 8:
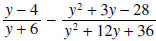
Solution: We must factor the denominators first to find the LCD:
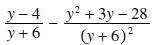
The LCD is 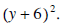 We now
convert each fraction to an equivalent fraction using this denominator:
We now
convert each fraction to an equivalent fraction using this denominator:
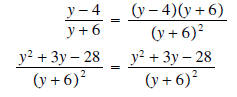
Next subtract the two expressions
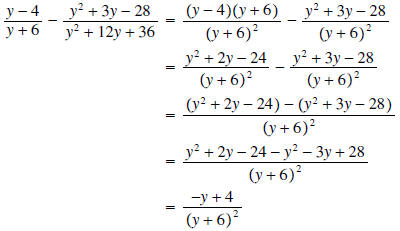
Note that the minus sign in the numerator was distributed across the expression
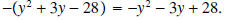
Question: What is the common denominator in
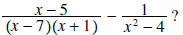
Answer:
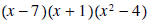
| Prev | Next |