Review of Trigonometric Functions
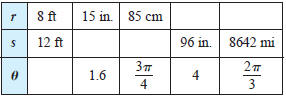
9. Let r represent the radius of a circle, θ the central
angle
(measured in radians), and s the length of the arc subtended by
the angle. Use the relationship 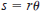 to complete
the table.
to complete
the table.
10. Angular Speed A car is moving at the rate of 50
miles per
hour, and the diameter of its wheels is 2.5 feet.
(a) Find the number of revolutions per minute that the wheels
are rotating.
(b) Find the angular speed of the wheels in radians per minute.
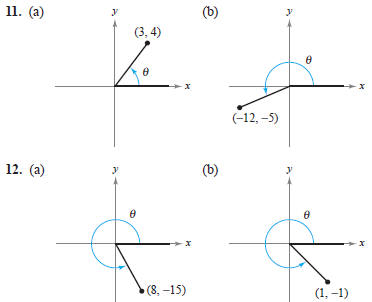
In Exercises 11 and 12, determine all six trigonometric
functions for the angle θ
In Exercises 13 and 14, determine the quadrant in which θ lies.
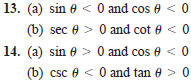
In Exercises 15–18, evaluate the trigonometric function .
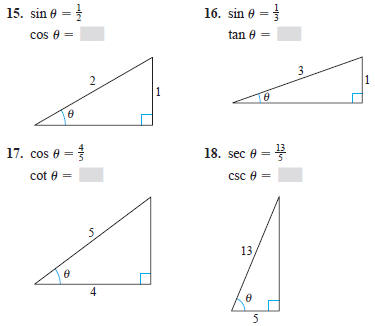
In Exercises 19–22, evaluate the sine, cosine, and
tangent of
each angle without using a calculator .
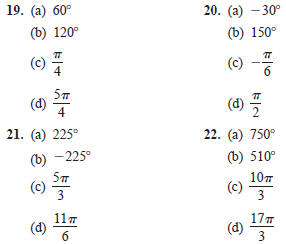
In Exercises 23–26, use a calculator to evaluate the
trigonometric
functions to four significant digits .
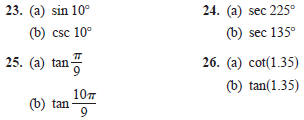
In Exercises 27–30, find two solutions of each
equation . Express
the results in radians(0≤θ<2π) Do not use a calculator.
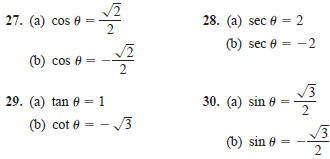
In Exercises 31–38, solve the equation for θ (0≤θ<2π)
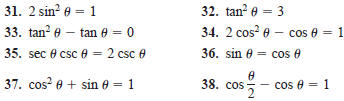
39. Airplane Ascent An airplane leaves the runway
climbing at
18° with a speed of 275 feet per second (see figure). Find the
altitude a of the plane after 1 minute.
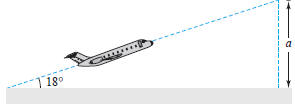
40. Height of a Mountain In traveling across flat
land, you
notice a mountain directly in front of you. Its angle of elevation
(to the peak) is 3.5° After you drive 13 miles closer to the
mountain, the angle of elevation is 9° Approximate the height
of the mountain.
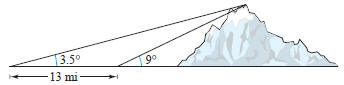
(not to scale)
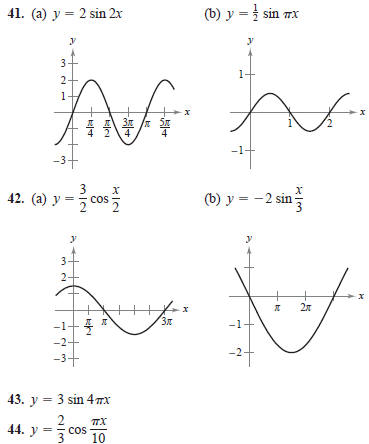
In Exercises 41–44, determine the period and amplitude
of each
function.
In Exercises 45–48, find the period of the function.

 Writing In
Exercises 49 and 50, use a graphing utility to
Writing In
Exercises 49 and 50, use a graphing utility to
graph each function f on the same set of coordinate axes for
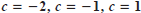 , and
, and 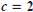 .Give a written description
.Give a written description
of the change in the graph caused by changing c.
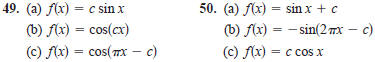
In Exercises 51–62, sketch the graph of the function.
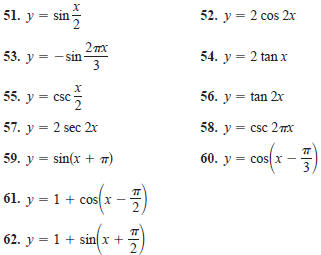
Graphical Reasoning In Exercises 63 and 64, find a, b,
and
c such that the graph of the function matches the graph in the
figure.
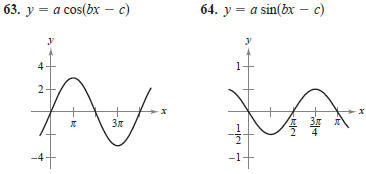
65. Think About It. Sketch the graphs of
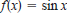 ,
,
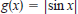 and
and 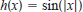 . In
general , how are the
. In
general , how are the
graphs of 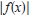 and
and
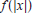 related to the graph of f?
related to the graph of f?
66. Think About It The model for the height h of a
Ferris wheel
car is
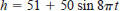
where t is measured in minutes. (The Ferris wheel has a
radius
of 50 feet.) This model yields a height of 51 feet when t=0
Alter the model so that the height of the car is 1 foot when
t=0.
 67. Sales Sales S, in thousands of units, of a seasonal
product are
67. Sales Sales S, in thousands of units, of a seasonal
product are
modeled by
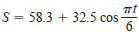
where t is the time in months (with t=1 corresponding to
January and t=12 corresponding to December). Use a graphing
utility to graph the model for S and determine the months
when sales exceed 75,000 units.
68. Investigation Two trigonometric functions f and g have a
period of 2, and their graphs intersect at x=5.35.
(a) Give one smaller and one larger positive value of x where
the functions have the same value .
(b) Determine one negative value of x where the graphs
intersect.
(c) Is it true that 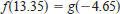 Give a reason for your
Give a reason for your
answer.
 Pattern Recognition
In Exercises 69 and 70, use a graphing
Pattern Recognition
In Exercises 69 and 70, use a graphing
utility to compare the graph of f with the given graph. Try to
improve the approximation by adding a term to Use a
graphing utility to verify that your new approximation is better
than the original. Can you find other terms to add to make the
approximation even better? What is the pattern? (In Exercise
69, sine terms can be used to improve the approximation and in
Exercise 70, cosine terms can be used.)
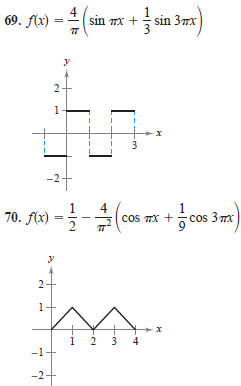
| Prev | Next |