Direct Proof
Ex. Give a direct proof of the following:
For every integer n, if n is odd then n^2 is odd.
Proof:
Let n be an odd integer.
Then n = 2k + 1 for some integer k.
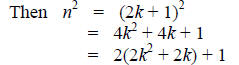
Therefore, n^2 is odd.
Ex. Give a direct proof of the following:
If r and s are rational numbers then r + s is a rational number.
Proof:
Let r and s be rational numbers .
Then r = a⁄b and s = c⁄d for some integers a, b, c, d with b ≠ 0 and d ≠ 0.
We then have
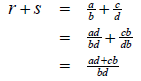
Note that ad+cb is an integer and bd is a nonzero integer.
Therefore r + s is a rational number .
Ex. Give an indirect proof of the following:
For every integer n, if n^2 is odd then n is odd.
Proof:
We will show ( n^2 is odd -> n is odd ) indirectly by showing ( n is even -> n^2
is even ).
We want to prove that if n is not odd, then n^2 is not odd.
Let n be an even integer.
Then n = 2k for some integer k.
Then
n^2 = 4k^2
= 2(2k^2)
Thus n^2 is an even integer.
Proof by Contradiction
Ex. Give a proof by contradiction of the following:
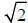 is irrational.
is irrational.
Proof:
Suppose that 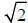 is not
irrational (suppose it is rational).
is not
irrational (suppose it is rational).
Then 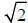 =a/b for some integers a and b.
=a/b for some integers a and b.
Without loss of generality we can assume that a/b is in reduced form ,
that is we can assume that a and b share no common divisor .
Square both sides to obtain
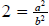 .
.
Then
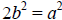 .
.
We now can see that 2 divides a ^2.
This implies that 2 divides a .
This implies that 4 divides a^2.
So, we can write a^2 as 4q for some integer q.
Our equation 2b^2 = a2 now becomes 2b^2 = 4q.
Thus b^2 = 2q.
So, 2 divides b^2.
Thus 2 divides b.
This is a contradiction. We assumed that
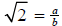 where a and b share no common divisor , yet we have arrived at the fact that a
and b must both be divisible by 2.
where a and b share no common divisor , yet we have arrived at the fact that a
and b must both be divisible by 2.
Therefore our assumption that
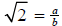 cannot be correct.
cannot be correct. 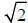 cannot be a rational
number . Hence
cannot be a rational
number . Hence 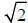 is irrational.
is irrational.
Proving “if and only if” statements
Ex. Prove that r is a rational number if and only if 2r is a rational number.
Proof:
(->)
First we shall show that if r is a rational number then 2r is a rational number.
Let r be a rational number.
Write r as a⁄b with a and b integers, b ≠ 0.
Then 2r = 2a⁄b . Since 2a and b are integers and b ≠ 0, we see that 2r is a
rational number
(<-)
Next we shall show that if 2r is a rational number then r is a rational number.
Let 2r be a rational number.
Write 2r as a⁄b with a and b integers, b ≠ 0.
Then r = a⁄2b . Since a and 2b are integers and 2b ≠ 0, we see that r is a
rational number.
We have now proved that r is rational iff 2r is rational.
Proving Statements are Equivalent
Ex. Show that the following are equivalent:
p1 : n is an even integer
p2 : n + 1 is an odd integer
p3 : n^2 is an even integer
Proof:
p1->p2
Suppose n is even. Then n = 2k for some integer k.
Then n + 1 = 2k + 1.
Thus n + 1 is odd.
p2->p3
Suppose n + 1 is odd. Then n + 1 = 2k + 1 for some integer k.
Then n = 2k.
Thus n^2 = 4k^2 = 2(2k^2).
Therefore n^2 is even.
p3->p1
We will show that n^2 is even -> n is even by an indirect proof (n is odd -> n^2
is odd).
Let n be an odd integer. Then n = 2k + 1 for some integer k.
Then n^2 = (2k + 1)^2 = 4k^2 + 4k + 1 = 2(2k^2 + 2k) + 1.
Thus, n^2 is odd.
We have now verified that these three propositions are equivalent .
Proof by Cases
Ex. Prove that the square of an integer ends with 0, 1, 4, 5, 6, or 9.
Proof:
Let n be an integer which ends in b. We can write n as follows: n = 10a + b.
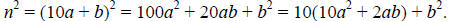
The last digit in the decimal expansion of n^2 is completely determined by b^2.
We need to examine b^2 for each possible value of b.
If b = 0 then b^2 = 0.
In this case the last digit of the decimal expansion of n^2 is 0.
If b = 1 or b = 9 then b^2 = 1 or b^2 = 81.
In either case the last digit of the decimal expansion of n^2 is 1.
If b = 2 or b = 8 then b^2 = 4 or b^2 = 64.
In either case the last digit of the decimal expansion of n^2 is 4.
If b = 3 or b = 7 then b^2 = 9 or b^2 = 49.
In either case the last digit of the decimal expansion of n^2 is 9.
If b = 4 or b = 6 then b^2 = 16 or b^2 = 36.
In either case the last digit of the decimal expansion of n^2 is 6.
If b = 5 then b^2 = 25.
In this case the last digit of the decimal expansion of n^2 is 25.
Thus, the last digit of n^2 must be either 0, 1, 4, 5, 6, or 9.
Existence Proofs
Ex. Use a constructive proof to show that there exists irrational numbers x and y such that x + y is rational
Proof:
Consider the irrational numbers
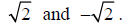
Note that
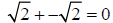 , and 0 is a rational number.
, and 0 is a rational number.
Ex. Use a nonconstructive proof to show that there exists irrational numbers x and y such that xy is rational.
Proof:
Consider 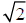 , which has been shown to be
irrational.
, which has been shown to be
irrational.
If 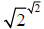 happens to be rational then we are done.
happens to be rational then we are done.
Suppose not, suppose 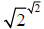 is irrational. Then
consider
is irrational. Then
consider 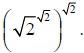
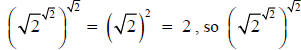 is rational.
is rational.
Ex. Prove that every odd integer is the difference of two perfect squares
Let n be an odd integer. Then n = 2k + 1 for some integer
k.
Note that
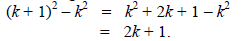
| Prev | Next |