Last₁

FACTORING TRINOMIALS USING THE ac METHOD

In order to factor using the ac method, the trinomial must be in the form ax^2 + bx + c, where a, b, and c are non-zero constants. As we proceed through our step-by-step explanation of how to factor a trinomial, we will use the following equation as our example:

6x^2 + 7x + 2 where a = 6, b = 7, and c = 2.

STEP 1: Factor out the Greatest Common Factor (GCF)

When factoring any expression, the first step is to factor out the Greatest Common Factor (GCF), if it exists. The GCF is the largest number or mathematical expression that will divide evenly into all the terms of the equation .

EX: 6x^2 + 7x + 2
In this case, there is no GCF because there is no number that will divide evenly into 6, 7, and 2, so we will move on to the next step.

STEP 2: Multiply the Values for a and c

EX: a = 6 c = 2 so 6*2 = 12

STEP 3: Find the Factors for the Result from STEP 2

We need to find the sets of factors for the result we obtained in STEP 2. Each set of factors will consist of any two numbers whose product equals the result.

EX:

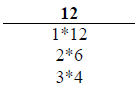
STEP 4: Determine which set of Factors Equals the Value of b

Once we have completed STEP 3 by finding all of the factors, we must decide which two to use to factor the trinomial. The factors we use will be the two whose sum is equal to the value of b in our equation.

EX:

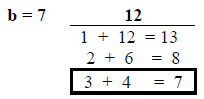
so, the factors we will use are 3 and 4.

STEP 5: Rewrite the Equation by replacing the second term with the two factors

EX: 6x^2 + 7x + 2 becomes 6x^2 + 3x + 4x + 2

NOTE: Remember to keep the variable x when you insert the factors into the trinomial.

STEP 6: Group the Terms

After inserting the factors, we need to group the terms before we continue to the next step. So, group the first two terms and the last two terms by underlining as in the example.

EX: 6x^2 + 3x + 4x + 2 becomes 6x^2 + 3x + 4x + 2

STEP 7: Factor out the GCF for each Group then Recombine the Groups

We must factor out the GCF from each underlined group.

EX: For the first group, the GCF will be 3x.

So, ( 6x^2 + 3x ) becomes 3x ( 2x + 1 )
For the second group, the GCF will be 2.
So, ( 4x + 2 ) becomes 2 ( 2x + 1 )

EX: 6x^2 + 3x + 4x + 2 becomes 3x ( 2x + 1 ) + 2 ( 2x + 1 )

NOTE: After factoring the GCF out of the two groups, the expressions in both sets of parentheses should match.

STEP 8: Factor the Expression Common to Both Groups

The final step is to factor out the expression that is common to both groups and place the remaining expression in parentheses .

EX: 3x ( 2x + 1 ) + 2 ( 2x + 1 ) becomes ( 3x + 2 ) ( 2x + 1)

FINAL ANSWER: ( 3x + 2 )( 2x + 1 )

Now, we will try another example:
Equation: 2x^2 – 11x + 15

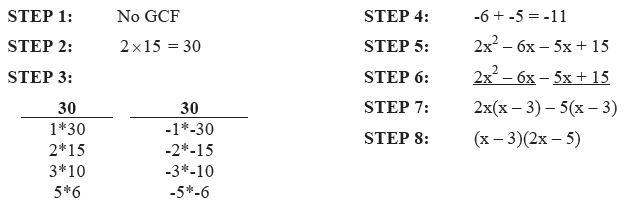
NOTE: In this example, the value of b is negative (-11) and the value of c is positive (+15), so we must use two negative factors.