SECTION 6.1 ELEMENTARY FRACTIONS

HOMEWORK: 1 – 37 odd, 39c, 41 – 59 odd

OBJECTIVES:
• Give examples of common uses of elementary fractions.
• Employs pictorial models to represent fractions and equivalent fractions .

1. What do you think of when you hear the word FRACTIONS?

2. A fraction is symbol a/b , in which a and b are numbers and b ≠ 0. If the numbers a and
b are whole numbers the fraction is called an ELEMENTARY FRACTION. a is called
the numerator and b is called the denominator. See bottom of page 268 for a brief
explanation of the reasoning behind the terms "numerator" and "denominator".

3. What are some different things in everyday life that the fraction 2/3 can represent?

4. See table on page 269 for a table that gives 4 meaning of an elementary fraction used
as a mathematical model .

5. Describe two ways to divide 5 brownies equally between 2 people.

6. A mixed number is a number that is made up of an integer and a fraction. For
example:

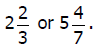a mixed number can also be written solely as a fraction.

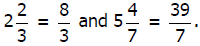When the numerator of a fraction is greater than the

denominator of a fraction , the fraction is called IMPROPER.

7. Using a variety of models, draw a picture to represent the following elementary
fractions.

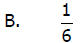
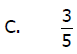
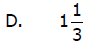
8. While children in elementary school study elementary fractions, children in middle
school also study the negatives of elementary fractions. The union of the set of
elementary fractions and
their negatives is the set of rational numbers .

RATIONAL NUMBERS are all numbers that can be written as a quotient (ratio) of two
integers p/q, in which q ≠0.

Which of the following are examples of rational numbers? Before you answer, think
carefully, is it possible to write the number as a ratio of two integers?

9. Draw a Venn Diagram that shows the relationships between the following sets of
numbers:

Rational numbers, Fractions, positive integers , elementary fractions
 

10. Equivalent Fractions are two fractions that represent the same rational numbers.
For example: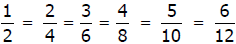

A. Represent the equivalent fractions using fraction bars (or strips).

B. Represent the equivalent fractions using number lines .

11. The Fundamental Law of Fractions :

A. Simplify Fractions : Write the following fraction in simplest form: 16/36.

B. Find an equivalent fraction for 2/3.

12. Compare and order Fractions

A. Which is larger 2/13 or 7/13?

B. Which is smaller 4/7 or 2/5?

13. The Denseness Property of Rational Numbers

A. Are there any fractions between 4/7and 5/7?