History of Math number

A mathematical proof is a way to show that some mathematical thing is true by using other
things that are understood to be true. A proof relies only on things that have already been proven. This
is what makes them proof. If the math a proof uses to prove something is in fact true, then the proof
makes no assumptions that make the proof doubtable.

Proof based mathematics differs from non-proof based mathematics because mathematics can
only be proof based if it relies only on mathematical facts to solve a problem . When solving a problem
using non-proof based mathematics, someone can simply decide that something makes sense intuitively
enough that they are convinced that it is correct. An example of the difference between proof based
mathematics and non-proof based mathematics is the difference between the Babylonian and Greek
understanding of the Pythagorean Theorem. The Greeks have done full proofs that show that the
Pythagorean Theorem is definitely true. They thought of the Pythagorean Theorem as a geometric
theorem, and proved it geometrically. They showed that two squares of area a^2 and b^2 equal a square
of area c^2, where a and b are the lengths of the sides of a right triangle and c is the length of the
hypotenuse of that right triangle. The Babylonians also appear to have understood the Pythagorean
theorem, even long before the birth of Pythagoras. As far as we know, the Babylonians did not provide
a general theorem for the theorem. The Babylonians understood what the Pythagorean Theorem later
proved, but could only explain it intuitively, and not by proof.

The Pythagorean theorem is an example of how important proof was to Greek mathematicians.
By using proof based mathematics, Greeks could build mathematical concepts on top of other
mathematical concepts. The understanding of geometric shapes that the Greeks had was far beyond the
Pythagorean theorem. They were able to build on top of the theorem because of the fact that it was
proven. Because the theorem was proven, other mathematicians could use it when making their own
proofs. Another good example of this is Euclid's Elements. The Elements are a list of mathematical
identities with proofs. They actually do build on top of each other. The Elements are many books filled
with mathematical propositions. If there were this many propositions all compiled together with no
proofs, it would be nowhere near as significant , because any error anywhere an any one of the books
could ruin the accuracy of a large portion of the rest of the books. Since Elements included proper
proofs, its contents are much more important to the world of mathematics.

Most higher geometry originated in Greece from when mathematicians tried to solve three
famous problems. These problems are the duplication of the cube, the trisection of an angle, and the
quadrature of the circle. These are examples of times when attempting to solve problems using proof
would be a mistake. That is because solving these problems is impossible. They can only be
approximated. Trying to solve these problems by proof would go nowhere. Greek mathematicians
solving these problems were only allowed to use a straightedge and a compass. There were strict rules
on how they were allowed to use these tools. When these tools are used following these rules they are
called Euclidean tools. These three famous problems are very important because the attempts to solve
them have lead to great improvements in mathematics. For example, it is believed that the conic
sections were invented in order to help solve the duplication of the cube problem. Since these
problems cannot actually be solved, none of them have proofs. Attempts at solving them have been
made using other techniques. This is a good example of how proof based mathematics can hinder
mathematicians in some situations. If these problems were ignored, because they cannot be proved,
many interesting mathematical discoveries and techniques would not be here today. Therefore, if the
Greeks only were willing to try problems that they could prove, they would have been doing the world
a disservice.

A good example of using proof is a sequence of proofs. One proof can lead into another proof,
and can be used to solve it. If you start by assuming that the area of a rectangle is the product of its
dimensions you can first prove that the area of a parallelogram is equal to the product of its base and
altitude. A parallelogram can be transformed to two two rectangles. From here we can use the fact that
a rectangle is the product of its dimensions to solve in the way shown below.

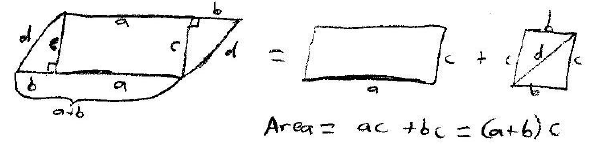
From here we can prove that the area of a triangle is equal to half the product of any side and
the altitude on that side. As shown below, two triangles can be placed next to each other to make a
parallelogram. This shows that the area of two of the same triangle is (a side of the triangle * altitude of
that side). Since we only want the area of one triangle, we can divide that area by two. This gives us
what we were trying to prove.

We can prove that the area of a right triangle is equal to half the product of its two legs similarly
to our last proof. When two of the same right triangle area put next to each other, they simply make a
rectangle. Since the area of a rectangle is the product of its dimensions, we can show this proof as
shown below.

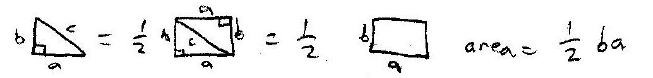
We can now prove that the area of a triangle is equal to half the product of its perimeter and the
radius of its inscribed circle. A triangle can be divided into six smaller triangles in the way shown
below.

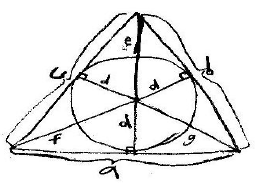
These six triangles can be doubled to become six rectangles in the same way right triangles
were turned into rectangles in the previous part of this proof. Using these rectangles, it can be shown
that the area is ½ (a + b + c) * d, which is half the product of its perimeter and the radius of its
inscribed circle.

We can now prove that the area of a trapezoid is equal to the product of its altitude and half the
sum of its bases. We will double every part of the trapezoid. This makes four rectangles this time. As in
the above two proofs we will add all of the triangles areas and divide by two, because everything was
doubled. This proof is shown graphically below .

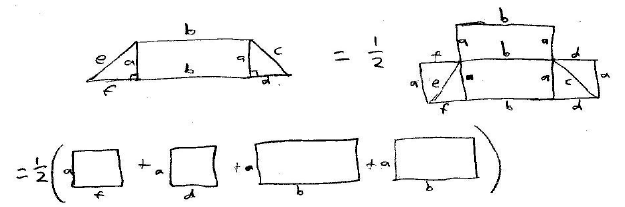
The area of this can be reduced to 1/2(b + b + f + d)*a which is the product of its altitude and
half the sum of its bases.

It can now be proven that the area of a regular polygon is equal to half the product of its
perimeter and its apothem. A regular polygon has n sides and can be turned into 2*n triangles. An
example showing this done for one side is shown below.

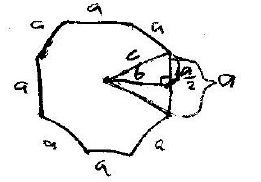
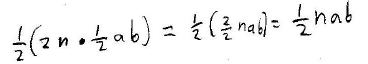
The area of the whole regular polygon is:
This shows that the area of a regular polygon is equal to half the product of its perimeter and its apothem.

The last part of the proof is t prove that the area of a circle is equal to half the product of its
circumference and its radius. This can be done using what was proven in the previous part if you think
of a circle as a regular polygon with infinity sides that are all infinitely small. The apothem could be
seen as the radius of the circle, since it goes to the center of an infinitely small side of the regular
polygon. The circumference can be seen as the perimeter since it's the sum of the infinitely many,
infinitely small sides. Therefore:

1/2(circumference * radius) = 1/2(perimeter * apothem)

So since the circumference of a circle is the same as the perimeter of a regular polygon, and the
radius of a circle is the same as the apothem of a regular polygon, the area of a circle is half the product
of its circumference and its radius.

This proof is a good example because it shows how one proof can help to make other proofs.
Also similar techniques that were used in earlier proofs can be useful again in later proofs.

A non-proof based mathematical conclusion to a problem is usually much easier to arrive at,
and if it makes sense, there is a good chance that it is accurate. However, if a non-proof based result
turns out to be incorrect, and others use that result to solve other problems, any number of later
problems could be solved incorrectly. This is the advantage of using proof based mathematics over
non-proof based mathematics. When proof based mathematics are used, there is no ambiguity and
every step taken uses only proven mathematical truths.

While proofs are good for formal purposes, they are often difficult to understand for someone
who is unfamiliar with what is being proven. For instance, the proofs in Elements could be very
difficult to understand for someone who hasn't been given an explanation. There are times when proofs
can be too formal, and descriptions that are easier to understand can be more useful. While proofs can
be difficult to understand, they are still very important or even necessary.

Solving a problem by proof seems like it is more for professional mathematicians. Proving a
solution is more necessary when trying to solve some kind of problem for the first time, because a
proof shows that the solution really works . Solving problems by proof isn't as necessary for students,
since they are solving mostly problems that have already been solved, and proven before. For a student,
it is useful to understand proofs, but simply being able to understand a problem, and solve it intuitively
might be a better solution. Solving by proof in many cases might be too overwhelming for a student.
Solving intuitively also makes more sense since a student is learning things for the first time, and
solving intuitively means that they understand the concepts.