Reminders:

Pick up materials (notes, slates, ...)
Grade your homework in red pen
Correct any problems you get wrong ask
a neighbor or two if you need help.

· Introduction to Factoring [ 5.1, p. 311 ]· #'s 15 60
( multiples of 5)

· Factoring Trinomials x ² + bx + c [ 5.2, p. 318 ]· #'s 10 55
( multiples of 5)

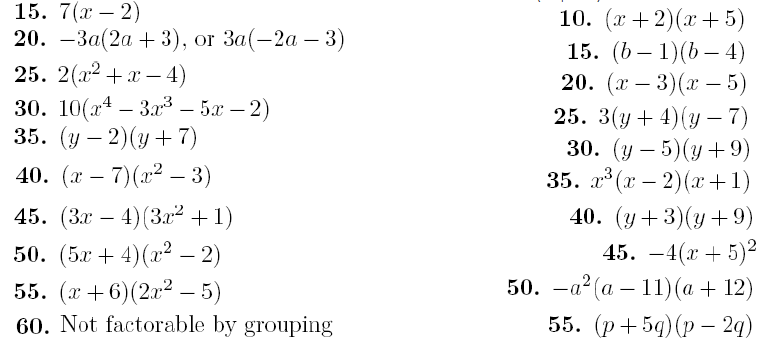
Schedule for today: 18 Oct

· Homework: Grade, Stamp, Turn in
· Reminder: Exam 2 Deadline today!
· Factoring Trinomials where a ≠ 1 [5.3]
· Factoring Difference of Squares [5.4]
· Begin Homework (if there's time)

Factoring ax ² + bx + c where a ≠ 1

So far, we have restricted our trinomial factoring to trinomials like :

x² -x-6
where the leading coefficient = 1

Factoring ax² + bx + c where a ≠ 1

Let's multiply two binomials to get a trinomial whose leading
coefficient is not equal to 1:

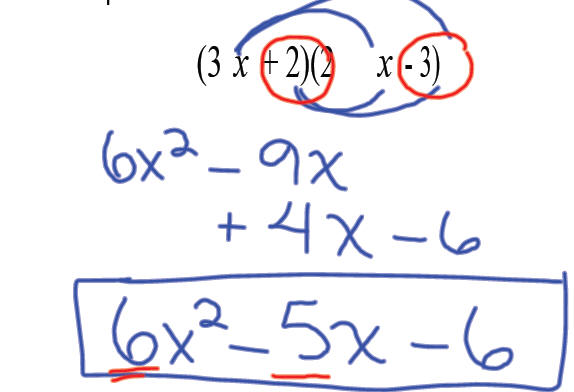
Note: when the leading coefficient ≠ 1,
the middle coefficient is not the sum
of the last two terms !

Factoring ax² + bx + c where a ≠ 1

Example 1: Factor -7x -15+ 2 x²

Factoring ax² + bx + c where a ≠ 1

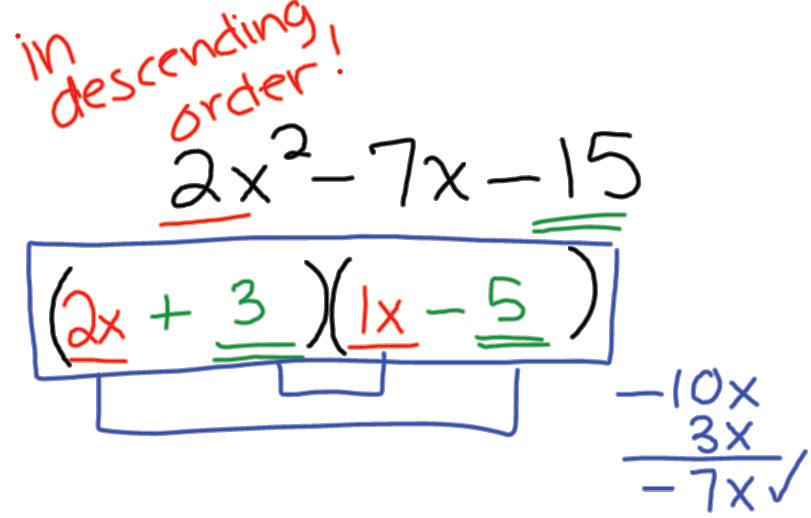
Example 2: Factor 3x²- x-2

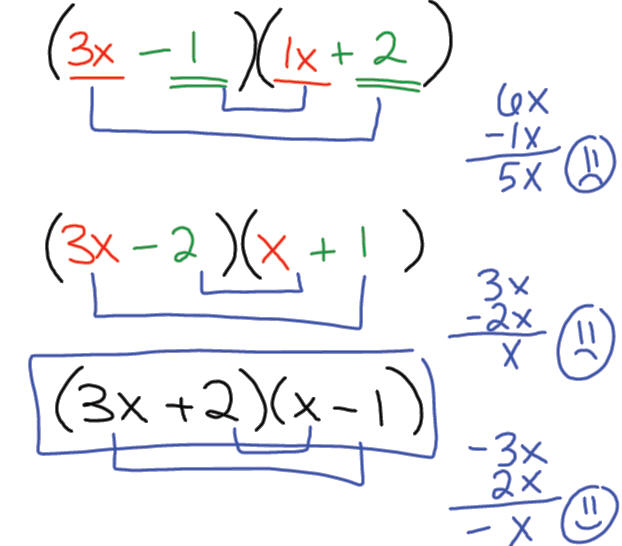
Factoring ax² + bx + c where a ≠ 1

Example 3: Factor 5x² -13x- 6

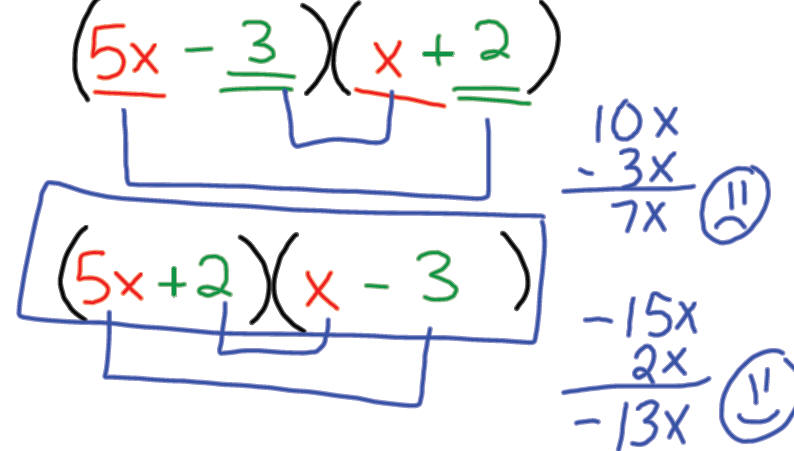
Factoring ax² + bx + c where a ≠ 1

Practice: In your notes, factor the following trinomials

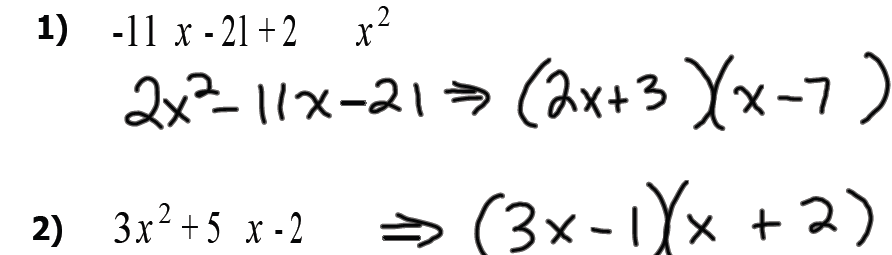
Schedule for today: Oct

· Homework: Grade, Stamp, Turn in
· Reminder: Exam 2 Deadline today!
· Factoring Trinomials where a ≠ 1 [5.3]
· Factoring Difference of Squares [5.4]
· Begin Homework (if there's time)

Difference of Squares

Note: Each of the terms in the binomials below is a perfect square

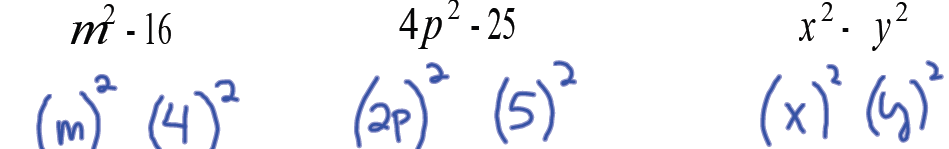
Difference of Squares

Observe: Factor m² -16

Difference of Squares

Rule for factoring the Difference of Squares:

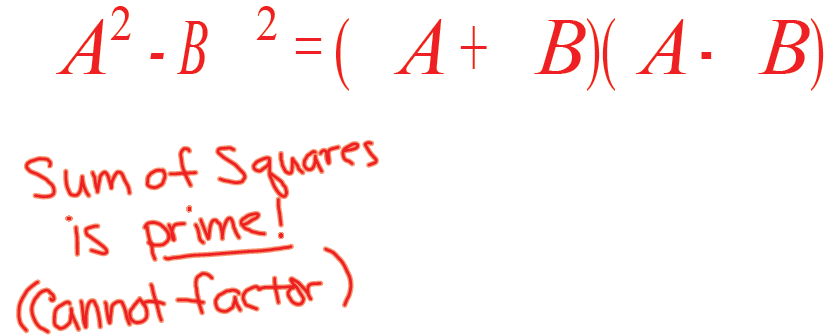
Difference of Squares

Example 1: Factor m²-16

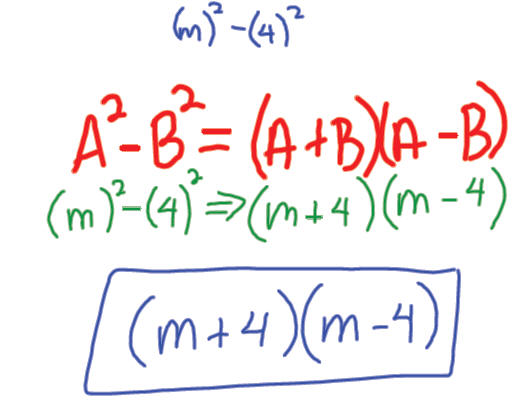
Difference of Squares

Example 2: Factor -4+x²
 

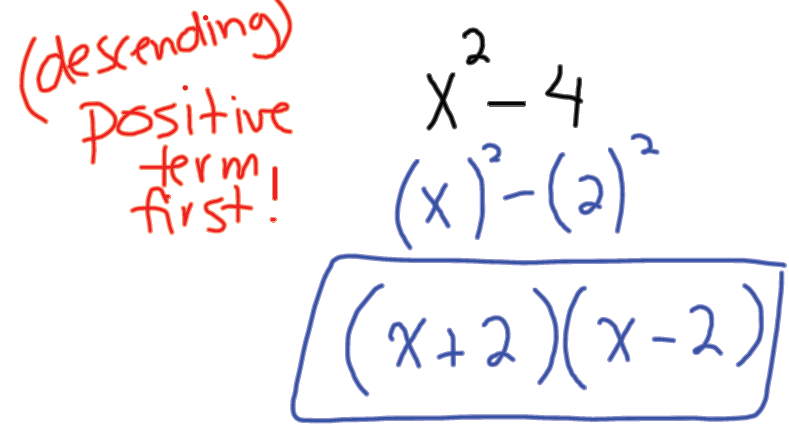
Difference of Squares

Example 3: Factor 49p²-a²

Difference of Squares

Example 4: Factor -36a² + 25y²

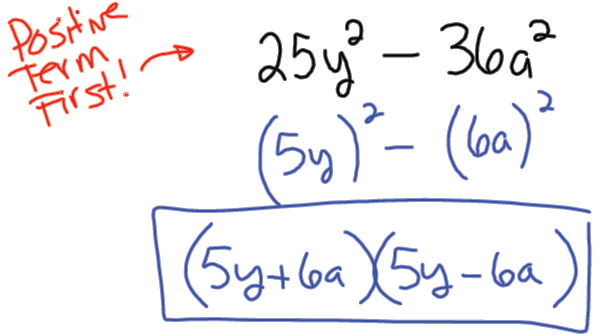
Difference of Squares

Example 5: Factor -36x⁶y⁴ + 49a²

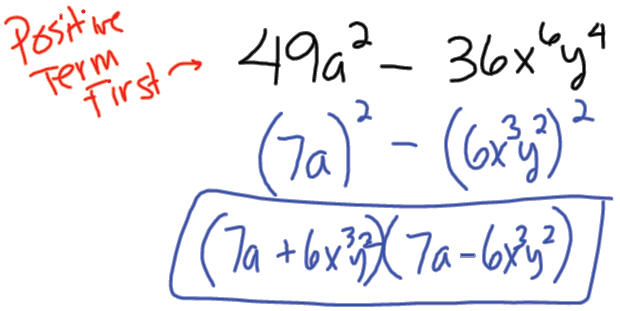
Slates! Slates! Slates!

Factor

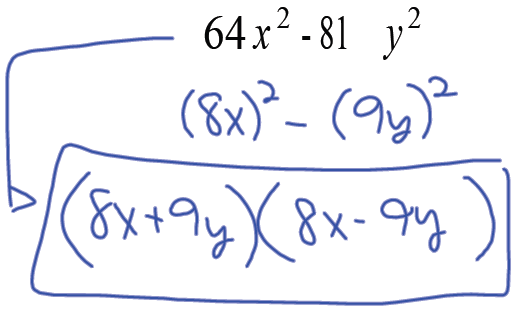
Slates! Slates! Slates!

Factor

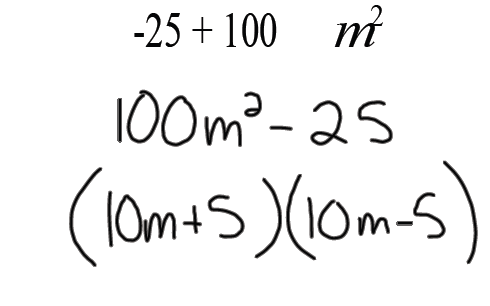
Slates! Slates! Slates!

Factor

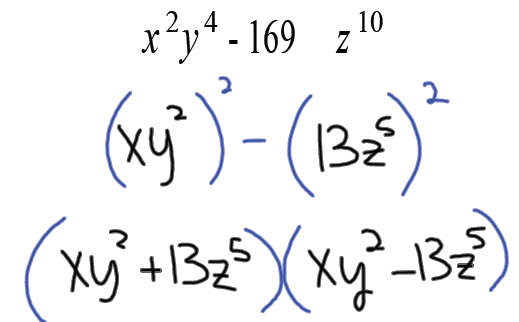
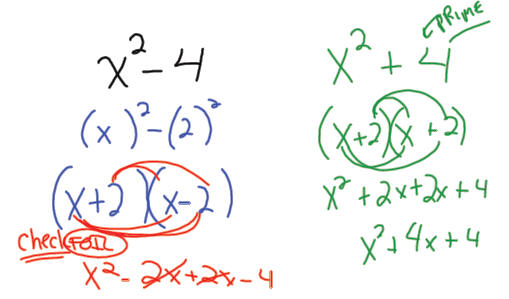
Have a great day!

Homework #16 (16 problems)
· Factoring Trinomials of the type
ax² + bx + c [ 5.3, p. 328 ]
#'s 5 45
(multiples of 5)
· Factoring Difference of Squares [ 5.4, p. 336 ]
#'s 57 75
(multiples of 3)