Fill the Number Grid
Fill the Number Grid
Objectives
The following number game is an excellent opening exercise for a whole
class to tackle. It is a discovery exercise in which all students can
participate.
As the grid is filled in, some patterns will emerge which can be seen even by
students who consider themselves 'weak' in math . Thus, everyone in the
class gets a chance to find a correct answer. But the actual rule for filling in
the grid also yields some results which may prove challenging to even the
math 'whizzes' in the class. [We will not reveal the rule for filling in the
grid
till later in the Procedure section, in case you would like to figure out
the
rule yourself first.]
Procedure
Present students with the following grid written on the
chalkboard. Their job
is to fill in the grid.
| 12 | ||||||||||||
| 11 | ||||||||||||
| 10 | 70 | |||||||||||
| 9 | ||||||||||||
| 8 | ||||||||||||
| 7 | ||||||||||||
| 6 | ||||||||||||
| 5 | 20 | |||||||||||
| 4 | ||||||||||||
| 3 | 24 | |||||||||||
| 2 | ||||||||||||
| 1 | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The ground rules for this game are similar to those for
What's the Rule?
Students make suggestions for numbers they would like to place in the grid.
The grid is set up like a set of coordinate axes , so students name the box they
would like to fill by saying the 'x' number first, followed by the 'y' number.
For example, box (4,5) has already been filled with the number 20. This
gives students practice for naming coordinates in a standard x, y graph . If a
student guesses a number correctly, that number is placed in the grid. We
make the rule that only students who raise their hands get to put numbers in
the grid. Students who just call out numbers are ignored. In this way, the
teacher can 'reward' specific students by allowing them to fill in several
numbers in a row once they find a specific pattern. It also makes it possible
to get more students involved, rather than letting a few aggressive students
dominate the action.
The three numbers that have already been placed in the
grid are a bit
misleading. They have been chosen to make it look like this is just a table of
multiplication facts . However, if you look at the completed grid below, you
will quickly see that this is not the case.
| 12 | 12 | 12 | 12 | 12 | 60 | 12 | 84 | 24 | 36 | 60 | 132 | 12 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 11 | 132 |
| 10 | 10 | 10 | 30 | 20 | 10 | 30 | 70 | 40 | 90 | 10 | 110 | 60 |
| 9 | 9 | 18 | 9 | 36 | 45 | 18 | 63 | 72 | 9 | 90 | 99 | 36 |
| 8 | 8 | 8 | 24 | 8 | 40 | 24 | 56 | 8 | 72 | 40 | 88 | 24 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 7 | 56 | 63 | 70 | 77 | 84 |
| 6 | 6 | 6 | 6 | 12 | 30 | 6 | 42 | 24 | 18 | 30 | 66 | 12 |
| 5 | 5 | 10 | 15 | 20 | 5 | 30 | 35 | 40 | 45 | 10 | 55 | 60 |
| 4 | 4 | 4 | 12 | 4 | 20 | 12 | 28 | 8 | 36 | 20 | 44 | 12 |
| 3 | 3 | 6 | 3 | 12 | 15 | 6 | 21 | 24 | 9 | 30 | 33 | 12 |
| 2 | 2 | 2 | 6 | 4 | 10 | 6 | 14 | 8 | 18 | 10 | 11 | 12 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The numbers in the grid are the Least Common Multiples
(LCM) of the bold
face numbers along the bottom and left axes. That is, 18 is the smallest
number that both 6 and 9 will go into evenly. 18 is also the smallest number
that 2 and 9 will go into evenly.
Example 1: You can get these least common multiples
by using a technique
that is sort of a repeated upside-down division. Example 1 shows this
technique for finding the least common multiple for the numbers 6 and 12:

First, divide both numbers by the smallest prime number (2) that will go into
both evenly. Write down the quotients 3 and 6 underneath 6 and 12,
respectively. Then divide both of those numbers by the smallest prime
number (3) that will go into them evenly. Again write down 1 and 2 under
them. Now multiply the divisors and the last two quotients together to get the
least common multiple : (2)(3)(1)(2) = 12. That is, 12 is the smallest number
that both 6 and 12 will go into evenly.
Example 2: Here is another example, finding the LCM
for 6 and 9:
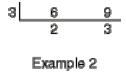
Only one division is possible. Therefore, the LCM is : (3)(2)(3) = 18.
Example 3: And here is an example for finding the
LCM for 2 and 9:
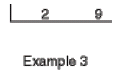
Since there is no number that goes into both 2 and 9 evenly, simply multiply
them together to get the LCM: (2)(9) = 18.
Examples 4 and 5: Here are two that require more
steps to show that you just
keep going till you cannot go any more:
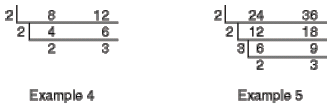
So the LCM for 8 and 12 is (2)(2)(2)(3) = 24. And the LCM for 24 and 36
is (2)(2)(3)(2)(3) = 72.
As you can see in the grid, there are some interesting
patterns. For example,
the main diagonal from lower left to upper right is the numbers themselves.
The left-hand column and the bottom row are all multiples of 1; therefore,
they are also the numbers themselves. Rows and columns involving prime
numbers (e.g., 7 and 11) do look like the simple multiplication facts, except
for the special cases of (7,7) and (11,11). These special cases, of course, can
be important clues to understanding the whole grid. Rows and columns
involving non-primes (e.g., 4s, 6s, and 12s) are the ones that are surprising
and/or confusing and, therefore, the most interesting.
Extensions
One teacher who used this exercise (Mary Hebrank, Duke
School for
Children) presented it a bit differently . She began the exercise as outlined
above, but then, since her students did not finish it right away, she devised a
poster with the grid on it. Students could come to her with their suggested
numbers, and if they were correct, she would add them to the grid with
post-it notes. The grid was finally filled after several days. Students were
also encouraged to write out and submit their explanations of how the grid
worked.
| Prev | Next |