MathEng 351

Study tips. To achieve minimal competency (C-) you must be able to do, without hesitation,
the first 3 problems from the exercises in the book of the sections we covered. To achieve prof-ficiency
(B-), you must be able to know how to apply the tools we have explored to problems
involving multi-step (four or more) conceptual calculations. To achieve excellence (A-) you must
be able to synthesize and interpret the information provided from multi-step calculations in order
to reach meaningful analytical conclusions. So, do every answered part of the first 3 problems of:
Chapter 2 sections 2-5, Chapter 3 sections 2-8, Chapter 8 sections 2-3, Chapter 9 sections 2-10,
Chapter 10 sections 2-6, Chapter 11 sections 2-5. Beyond that, make sure you can do without
hesitation all the problems on the midterms. Then review the rest of your homework assignments.
Stick to the problems that have answers in the back so you can check your work. I will be available
to help with the questions that don’t have answers in the back.

Topics

(1) Chapters 1-3: ODE’s

(a) Classification: n’th order, (non)linear, (non)homogeneous, (non)constant coefficients,
separable equations, exact equations, Cauchy-Euler equation, systems
of ODE’s.

(b) Solution techniques :
• exact equations (for certain first- order ODEs ),
• separation of variables , (for first order separable equations),
• variation of parameters (for first or second order, nonhomogeneous linear
ODE’s),
• reduction of order ,
• second-order linear homogeneous ODE’s with constant coefficients
(know what to do with the characteristic polynomial/ equation and repeated
roots, know what linear independence of general solutions means and how to
test for/generate linearly independent solutions, know how many linearly independent
solutions to expect for a general nth order ODE, know the difference
between the general solution expressed as a linear combination of n linearly independent
functions (Theorem 3.3.2) and an exact solution satisfying given
initial/boundary conditions),
• method of undetermined coefficients (for second order nonhomogeneous
equations),
• techniques for solving equations of Cauchy-Euler-type (nonconstant, algebraic
coefficients, know what to do with repeated roots for the characteristic
equation),
• matrix techniques (for solving systems of ODE’s or for transforming higherorder
ODE’s into systems of first-order ODE’s).

(c) Theorems/Definitions:
• existence/uniqueness for first-order ODE’s and initial value problems ,
• domain and range of solutions to ODE’s,
• initial/boundary conditions,
• homogeneous solution,
• (linear) differential operators (equation 3.3.8),
• linearly (in)dependent functions (Theorems 3.2.4 and 3.2.5, 3.4.1),
• Wronskians (Theorems 3.2.1, 3.2.2 and 3.2.3),
• characteristic polynomial/equation (repeated roots)
• particular solution,
• general solution,
• a basis for the general solution,
• exact solution,
• (natural) frequency of the harmonic oscillator,
• amplitude and phase of the harmonic oscillator,
• damping/forcing of the harmonic oscillator,
• resonant forcing.

(d) Formulas for general solutions: there are general solutions to homogeneous and inhomogeneous
first order ODE’s (equation 2.2.21 and 2.2.24). There is also a formula for
second order nonhomogeneous ODE’s with constant coefficients that involves Wronskians
(equation 3.7.49). You may use these formulas, provided you know how.
(e) Applications: population dynamics, chemical kinetics, the harmonic oscillator, everything
else under the sun. Something to figure out how to answer: if the roots of the
characteristic polynomial of an ODE describing a population of locusts in sub-Saharan
Africa are real and greater than zero, then what will be the long-time behavior of the
locust population? Should governments be worried?

(2) Chapters 8-11: Linear Algebra

(a) Know the difference between a vector space and a set of vectors.

(b) Know the difference between a basis and a generating set of a space.

(d) Know the difference between lineraly (in)dependent vectors and linerly (in)dependent
functions.

(e) Know the difference between scalar multiplication and matrix /vector multiplication.

(f) Know the difference between a space and a subspace.

(g) Know the difference between the dimension of a space and the span of a set of
vectors.

(h) Know the difference between the rank of a matrix and the dimension of a space.

(i) Know the meaning of the following statement: Two subspaces of a general space S can
have the same dimension without being the same subspace.

(j) Matrices A 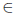R^m×n.
• Know the following classes of matrices: square , upper (lower) triangular,
(block) diagonal, invertible, singular, full rank, diagonalizable, row
equivalent.
• Know the properties of and how to calculate the following operations: transposition
(Theorem 10.3.1), determinants (Properties D1-12), scalar multiplication,
matrix addition/multiplication (Theorems 10.2.1-3), left/right matrix
multiplication, rank (Theorems 10.5.1-2), elementary row(column)
operations, inversion (adjoint formula, ”parallel” elementary row operations).
• Know how to calculate and interprate eigenvalues and eigenvectors, roots
of the characteristic polynomial.
• Symmetric matrices. Know the properties of these special matrices
(Theorems 11.3.1-4).
• Diagonalization.
– Know the relation between the eigenvectors/values of a matrix and it’s diagonalizability.
Know the advantages of symmetric matrices with respect
to diagonalization.
– Know and understand the statements of Theorems 11.4.1-4.
• Know what the nullity of a matrix, how to compute it, what this has to do
with finding the eigenvalues of a matrix, and what this has to do with solving
homogeneous systems of equations.
• Know how to calculate the rank of a matrix.

(k) Vectors x 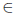Rⁿ (that is, rank 1 matrices). Know the following terminology and know
how to calculate:
• vector space,
• span,
• basis (Definition and Theorem 9.9.1),
• generating vectors,
• dimension (Definition and Theorem 9.9.2, Theorem 9.9.4)
• orthogonal,
• linerly independent,
• unit,
• orthonormal,
• expansion of any given vector u in terms of an orthogonal (orthonormal)
basis (equations 9.9.23-24),
• norm (Euclidean),
• dot (inner or vector) product ,
• triangle inequality ,
• Schwarz inequality,
• angle between vectors,
• eigenvectors,
• best approximation (equation 9.10.5).

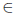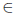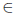(l) Systems of linear equations, that is Ax = b where A R^m×n x Rⁿ, b R^m.
• consistent/inconsistent systems of equations.
• Existence/Uniqueness for linear systems (Theorems 8.3.2-4)
• Know how to use Gauss-Jordan reduction to solve systems of equations.
• Know and understand the statements of Theorems 10.5.3-5.
• Know when to and be able to use matrix inversion and Cramer’s Rule for
solving systems of equations (see Theorem 10.6.2).
• Applications: solving systems of linear algebraic (polynomial) equations,

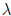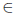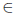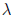
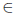(m) Eigenvalue problems, that is Ax = x where A R^m×n x Rⁿ, C.
• Be able to calculate the eigenvalues and eigenvectors
• Know the relation between the roots of the characteristic polynomial of A and
the eigenvalues of A.
• Know how to find and express (in terms of some basis) the eigenspace corresponding
to a particular eigenvalue of A.
• What does it mean to have an eigenvalue 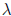= 0? How does this relate to the
rank/nullity of A? How does the number (together with multiplicities) of nonzero
eigenvalues relate to the rank of A?
• Understand the relation between the multiplicity of an eigenvalue and the dimension
of the corresponding eigenspace (the dimension of the eigenspace will
allways be less than or equal to the multiplicity of the eigenvalue. Moreover, the
dimension of the eigenspace will allways be at least 1).
• Be able to give a graphical interpretation of the eigenvectors/values of A.
• Know the properties of eigenvalues and eigenvectors of symmetric matrices (Theorems
11.3.1-4).
• Know how eigenvalue problems arrise in the solution of systems of linear ODE’s
and be able to interpret the eigenvalues/vectors of the matrix A in terms of the
dynamical behavior of the corresponding system of ODE’s. In particular, be
able to interpret the eigenvectors of a system of ODE’s in terms of it’s natural
modes (problem 11.3.8 and 11.4.5).