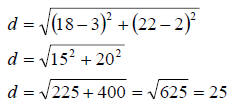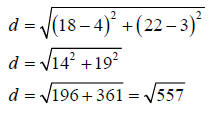Finding the Distance Between Two Points

Suppose we want to find the distance between the two points
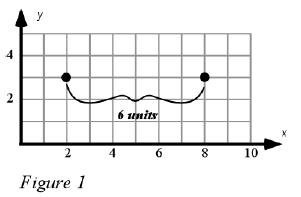
(2, 3) and (8, 3). We can plot the points on a grid (see Figure 1) and then count the number of squares from one point to the other. The distance between these two points is 6 units. Since these two points are located on a horizontal line, we can calculate the distance between them by finding the difference between their x-coordinates: 8 – 2 = 6.

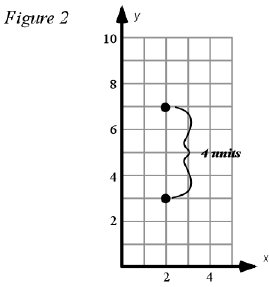Similarly, the distance between two points located on a vertical line can be calculated by finding the difference between the y-coordinates of the two points. The distance between the points (2, 3) and (2, 7) is 4 units (see Figure 2) which can be calculated: 7 – 3 = 4. The coordinates of a point may be generalized (x, y). Subscripts are used to indicate the coordinates when two points are generalized i.e., (x1,y1) and (x2,y2). The calculation for the distance between two points on a horizontal line, then, may be generalized as x2−x1, and for two points on a vertical line the distance is, y2−y1

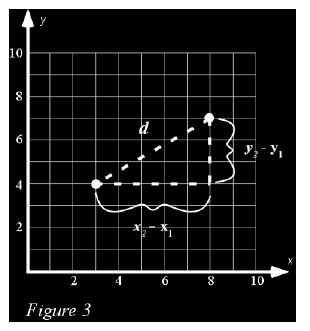
Figure 3 shows two points that are located neither on a horizontal line nor on a vertical line. We can use the Pythagorean relationship to determine the distance between the two points. The horizontal distance, x2−x1, is 8 – 3 = 5 and the vertical distance y2−y1, is 7 – 4 = 3. A right triangle is formed by the sides x2−x1, y2−y1, and hypotenuse, d, (see Figure 4). We can use the Pythagorean Theorem to determine the distance, d between the two points as follows:

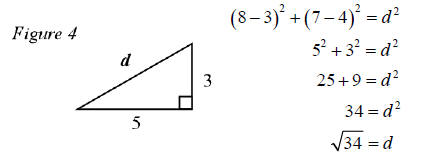
We can generalize a formula for finding the distance between any two points based on the Pythagorean Theorem as follows: Distance Formula:

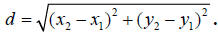
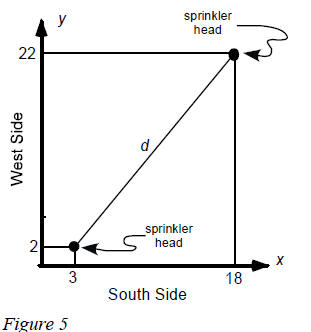
Problem: Suppose a plumber is at the store buying materials to install a sprinkler system on a rectangular lawn as shown in Figure 5. He needs enough pipe to connect two sprinkler heads but he forgot to measure the distance between them. He knows where they are in the lawn, however. One is 3 feet from the west side and 2 feet from the south side. The other is 18 feet from the west side and 22 feet from the south side. He can put his math 70 skills to work to find the distance between the sprinkler heads without going back to measure.

Solution : If we let the west side of the lawn be the y-axis and the south side of the lawn be the x-axis (see Figure 5) then the first sprinkler head is at the point (3, 2) and the other is at the point (18, 22). The distance between the sprinkler heads is represented by d. Using the distance formula, The sprinkler heads are 25 feet apart.

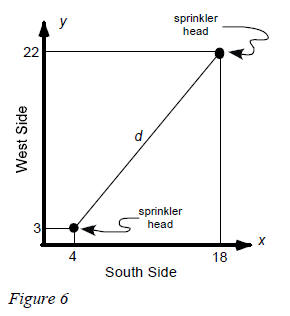
Problem: Will we always get such a nice, rational number? No. Let’s take the same sprinkler head problem as above, but this time let us say that the sprinkler heads are placed 4 feet from the west side and 3 feet from the south side. The other sprinkler is still 18 feet from the west side and 22 feet from the south side as shown in Figure 6. Let’s put our math 70 skills to work to find the distance between the sprinkler heads without going back to measure.

Solution : If we let the west side of the lawn be the y -axis and the south side of the lawn be the x-axis (see Figure 6) then the first sprinkler head is at the point (3, 2) and the other is at the point (18, 22). The distance between the sprinkler heads is represented by d. Using the distance formula,

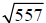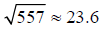Now, is not a rational number . If we round our answer to one decimal place then we can say that the sprinkler heads are feet apart. We might want to go one step further and say that the sprinkler heads are 23 feet and 7.2 inches apart.

Homework:

1. Plot the points (2, 5) and (8, 5) on the grid at right. Determine the distance between the points by counting squares . 2. Use the distance formula to determine the distance between the points (2, 5) and (8, 5). Show your work. Does your answer agree with problem #1? (it should!)

Use the distance formula to find the distance between the following pairs of points. Round answers to two decimal places .

Answers:

1. 6 units
2. 6 units, yes! they agree!
3. 5
4. 6.40
5. 7.81
6. 5.39
7. 13.04
8. 4.37