Math 1120 Exam Review 2
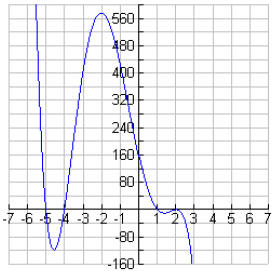
1. Write a formula for a linear function that has a slope
of 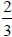 and passes through the point (‐6,4).
and passes through the point (‐6,4).
2. Write a formula for the linear function that models the following situation.
Clearly indicate
what the variables represent and find the domain: In 1992, the rate of injury
cases recorded in
private industry per 100 full‐time workers was 8.3 and it decreased on average,
by 0.32 injuries
every year until 2001.
3. Find the equation of the line passing through (4,7) and (‐2,‐3). Write your
answer in slope ‐
intercept form .
4. Find the equation of the line through (2,‐5) that is parallel to 3x + 2y = 6.
Write your answer in
slope‐intercept form.
5. Find the equation of the line through (2,3) that is perpendicular to 2x + y =
‐3. Write your
answer in slope‐intercept form.
6. Given the point (2,5) , find:
a. The equation of the vertical line through it.
b. The equation of the horizontal line through it.
7. The weight of an object on Earth is directly proportional to the weight of an
object on Mars. If a
25‐pound object on Earth weighs 10 pounds on Mars, how much would a 195‐pound
astronaut
weigh on Mars?
8. Solve for the given variable:
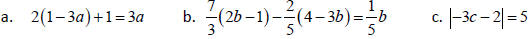
9. Solve for the given variable and classify the equation
as a contradiction, and identity, or a
conditional equation.
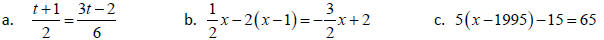
10 . A radiator holds 5 gallons of fluid. If it is full
with an 80% antifreeze mixture, how much fluid
should be drained and replaced with water to result in a 50% antifreeze mixture?
11 . At 2:00 p.m., a runner heads north on a highway jogging at 10 miles per
hour. At 2:30 p.m., a
driver heads north on the same highway to pick up the runner. If the car travels
at 55 mph.,
how long will it take for the driver to catch the runner?
12 . Solve the following inequalities. Express your answers in interval
notation.
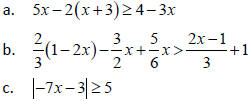
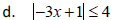
13. The number of Harley ‐Davidson motorcycles manufactured
between 1985 and 1995 can be
approximated by 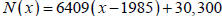 where x is the year.
where x is the year.
a. Did the demand for Harley‐Davidson motorcycles increase or decrease over this
time
period? Explain your answer.
b. Estimate the years when production was between 56,000 and 75,000
14. For the following piecewise‐defined function,
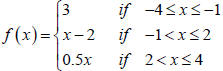 find:
find:
a. The domain of f.
b. 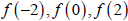 , and
, and 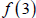
15. Write 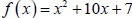 in the form
in the form
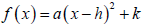 and identify the vertex.
and identify the vertex.
16. Solve the quadratic equation : 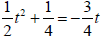
17. Solve by completing the square: 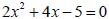
18. Use the discriminant to determine the number of real solutions and then
solve the quadratic: .
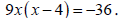
19. The cost , C, in dollars of manufacturing x scooters at Scooter Productions
is given by .
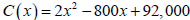 Find the number of scooters that must be
manufactured to
Find the number of scooters that must be
manufactured to
minimize the cost.
20. Given the function 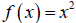 and the function
and the function
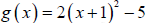 . Describe the
. Describe the
transformation used to create g(x) from f(x).
21. Indicate the intervals for which the function
(shown at the right)
is increasing, decreasing, or constant.
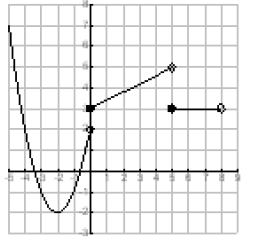
22. Classify the following functions as even, odd, or neither:
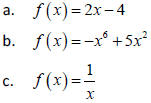
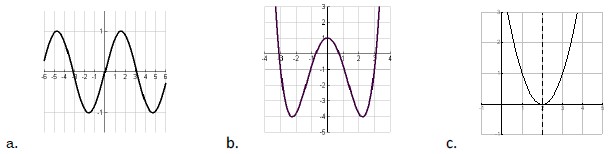
23. . Classify the following functions as even, odd, or neither:
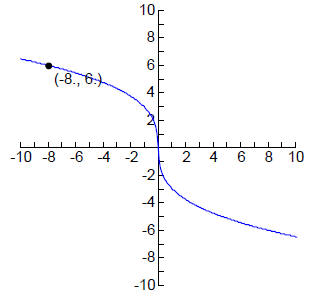
24. Use the point shown to determine a second point (other than the origin) on the graph:
Calculator Content :
25. The following table lists the outstanding balances on Visa and
MasterCard credit cards in
billions of dollars.
| Year | 1980 | 1984 | 1988 | 1992 | 1996 |
| Balance | 82 | 108 | 172 | 254 | 444 |
a. Use your calculator to produce a scatterplot of the
data, letting x represent the number of
years since 1980.
b. Determine whether a linear or quadratic function would best fit the data.
c. Graph the function with the scatterplot.
d. Use your model to predict the outstanding balance in 1999 and 2003.
26. For the polynomial 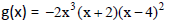
a. Find the zeros of the polynomial function and state the multiplicity of each.
b. What is the most number of turning points that might be present in the graph
of g(x)?
c. Identify the leading term and end behavior for the function
27. Write the complete factored form of 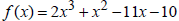 given that k=-2 is a zero.
given that k=-2 is a zero.
28. Given: 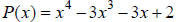 and
and
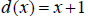
a. Use long division to find the quotient and remainder when P(x) is divided by
d(x).
b. Find the remainder when P(x) is divided by d(x) using the Remainder Theorem.
29. Determine the equation of the polynomial of lowest degree whose graph is
given below. (x‐scale: 1
interval = 1 unit; y‐scale: 1 interval = 40 units). You do not need to multiply
out the factors .
Key:
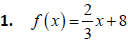
2. X = year; 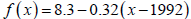 ; Domain =[1992,2001]
; Domain =[1992,2001]
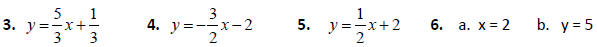
7. 78 pounds
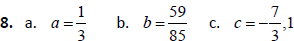
9. a. No solution, Contradiction
![]() b. All real numbers ,
Identity
b. All real numbers ,
Identity ![]() c. x = 2011,
Conditional
c. x = 2011,
Conditional
10. 1.875 gallons
11. Driver will travel 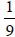 hour or approx.
hour or approx. 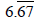 min.
min.
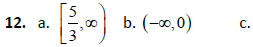
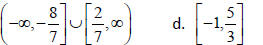
13. a. Demand increased since the slope is positive .
![]() b. Between about 1989
and 1992.
b. Between about 1989
and 1992.
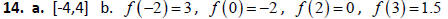
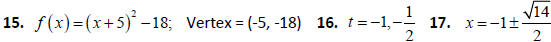
18. Discriminant = 0, one real solution, x = 2.
19. X = 200
20. Starting with f(x), the graph is shifted to the left 1 unit, vertically
stretched by a factor of 2, and shifted downward 5 units.
21. Inc. [‐2, 5) Dec. (‐∞, ‐2] Constant [5, 8)
22. a. Neither. ![]() b.
Even,
b.
Even, ![]() c. odd
c. odd
23. a. odd, ![]() b. even,
b. even,
![]() c. neither
c. neither
24. (8, ‐6)
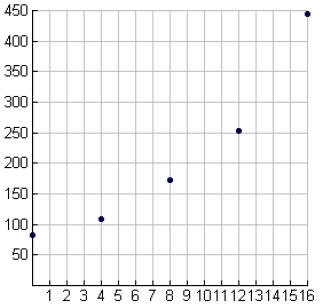
25. a.
b. Quadratic is best fit.
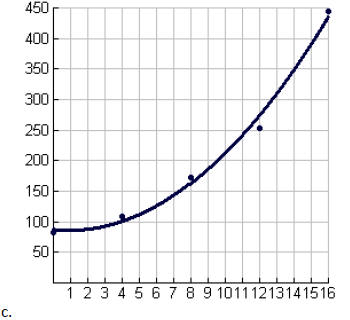
d. For 1999, about 588.7 billion, and for2003, about 836.3
billion
26. a.) x=0, with mult. 3; x=-2, with mult. 1: x=4, with mult. 2

 ,both ends
down.
,both ends
down.
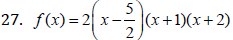
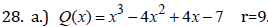
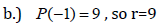
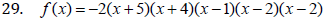
| Prev | Next |