First-order Linear Equations-Examples
1. Homogeneous: y' + p(t)y = 0, y = y(t). We assume p(t)
continuous
for t > 0. We always have:
i) solutions of the IVP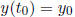 
with
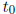> 0 are defined for all t > 0,
ii) solutions are either positive for all t > 0, negative for all t > 0, or
zero for all t (depending on the sign of
),
iii) if p(t) doesn't change sign , y(t) is either monotone increasing or
monotone decreasing.
Ex.1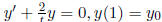 
. The solution is :
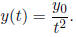
Solutions are increasing for
< 0, decreasing for
> 0, in either case, the
asymptotic value is zero .
Ex.2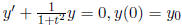 
. The solution is:
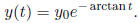
Thus if > 0 solutions are decreasing, with asymptotic values
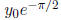(as
t → +∞),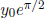 
(as t → -∞).
Remark. In general, the asymptotic value as t → +∞ will be non-zero
( positive if > 0) when the following improper integral converges:
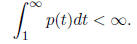
Ex.3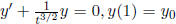 
. We expect solutions with
> 0 will be
positive, decreasing and have positive asymptotic value (using the criterion
just mentioned.)
Indeed, the solution is: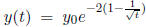 
, with the limit
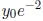as
t → ∞.
So far the solutions have been monotone. To get oscillations, we consider
examples where p(t) is oscillatory.
Ex.4a. y' + (sin2t)y = 0, y(0) = 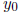. The
solution is:
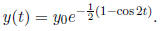
Since cos 2t oscillates between -1 and 1, the solution y(t)
oscillates between
the constant positive values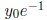 
and
.
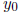Ex. 4b. y' + (3 + sin t)y = 0, y(0) = 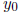. Here
p(t) is everywhere positive
(although it oscillates with mean value 3), so we expect solutions with
> 0
will be positive, monotone decreasing, with asymptotic value zero . Indeed
we find:
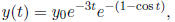
which alternately touches the curves ( decreasing exponentials ):
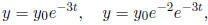
while remaining strictly decreasing (as t → +∞). It doesn' t really 'oscillate'.
2. Non- homogeneous equations . y'(t)+ p(t)y = f(t). Assuming p(t) and
f(t) continuous for t > 0, the solutions will be defined for t > 0. Beyond
that, there is little one can say in general. The general solution is:
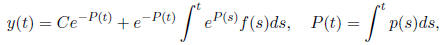
which has the form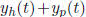 
(
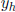is the solution of the associated homoge-
neous equation .) The integral defining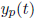 
is often impossible to compute
explicitly.
Ex.5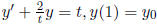 
. The solution is:
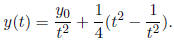
With > 0, y(t) tends
to infinity as t → 0 and t → +∞, and has a unique
minimum at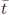 
> 0, with
.
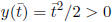Ex.6 y' + 3y = e7t, y(0) =
. Solution:
.
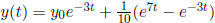Ex.7 y' + 2ty = t, y(0) =
. The solution is:
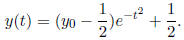
All solutions are even functions, defined for all t ∈ R, and tending to
the
constant solution 1/2 as t →±∞: Incidentally, the constant solution can be
found directly, simply by setting y' = 0 in the equation:
2ty = t => y ≡ 1/2.
| Prev | Next |