Math Assignment 2

One major approach to the problem of simplification of mathematical expressions is to define
and maintain a canonical form valid over some interesting class of expressions as elements
in that class are manipulated. In this problem set you will devise and analyze a canonical form
for sc-series (sine-cosine series), a class of expressions we have invented for these exercises, but
resembling so-called “Poisson” series used in Macsyma, CAMAL, and some other systems .
Such series are typically highly useful in celestial mechanics (for orbital calculations) but are
sometimes used for ( mathematically similar ) differential equations problems that occur in
other disciplines.

We’ll define sc-series through the following sequence of informal definitions (If you need
clarification or more formalism, ask):

• a variable is any alphanumeric name except for the literal “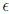 ” which we reserved for
later use. Examples: x, y, t45.
• a rational number is an integer or a pair of integers, numerator and denominator , in
some suitable notation.
• a term is a rational number times a variable. Note that unless it causes confusion, we
will denote multiplication by juxtaposition of symbols. Examples: 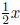, 3 t45.
• an arg is a sum of one or more terms . Example:
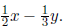
• a trigform is a rational number times a non-negative power of the symbol times sin
or cos of an arg. One example: 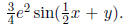Another example:

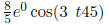
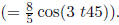
• an sc-series must be able to represent any sum of trigforms.

We will not formally specify the meaning of these expressions, but they are meant to
correspond to the usual applied-mathematics notions of computations over rational complex
numbers, indeterminates (to the extent you need to be aware of this, the indeterminates
denote complex numbers , and not, say, matrices), and the trigonometric functions. The
common interpretation of trig functions should tell you what we mean by differentiation, for
example.

1. In order to make sure that any two equivalent expressions are identical if expressed as
sc-series, a number of other constraints must be placed upon the form. For example we could
insist that the terms in the arg are in alphabetic order by variable name, and there are no
duplicate names. What other constraints do you recommend, and why? (You may interpret
this question as requiring you to eliminate the informality in the above specifications.)

2. How do you propose to represent rational constants ? How about zero? The constant
is not available in this representation. What would happen if it were?

3. In order to make some use of sc-series, we need to develop programs for the following
operations:

Given an sc-series s, we must be able to compute the derivative or the integral of s with
respect to some variable v. (The result must also be in canonical form, of course.)

Given two sc -series s and t, we must be able to compute their sum, their product, and
their difference .

While you need not actually write these programs (although you may if you wish), provide
enough of a pseudo-code description to demonstrate that you’ve addressed all important
mathematical or representation issues. In particular, you should characterize the costs of
running these programs, stating any assumptions you are making along the way.

4. There is a transformation which preserves equivalence only approximately turns out to
be of some use. Given a series s 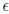, expand it in a new series s' where a particular variable,
say x is known to be a small quantity, . Then an integer degree d is chosen and sin x and
cos x are expanded in power series to degree d. For example, if d = 3, then sin(x + y) is
(approximately) 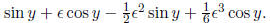The dependence on x is changed from
trigonometric to algebraic. Explain how to do this. (Pseudo-code algorithm, cost)

5. Computing u := s⁴ can be done by computing t := s * s and then u := t * t. Or it can
be computed by t := s * s, v := s * t, and finally u := s * v. Discuss which is better. This
requires that you refer to your cost model of multiplication of sc-series (in answer to question
3) carefully. You will probably have to specify how you are storing sc-series. You should also
make some statements about the maximum, minimum, and/or likely sizes of s, t, u, and v in
order to complete your analysis.